행렬 분해(Matrix Decomposition) 종류

1) 고유값 분해(Eigen Value Decomposition)
2) 스펙트럼 분해(Spectral Decomposition)
3) 특이값 분해(Singular Value Decomposition)

---

1) 고유값 분해(Eigen Value Decomposition)

- 모든 대칭 행렬 A에 대해 고유값 분해(EVD, Eigen Value Decomposition, Spectral Decomposition)가 가능함을 보았다.

$$ A = P D P^T $$

Eigen Value Decomposition

 

※ 모든 N x N 정방행렬 A가 고유값 분해가 가능한 것은 아니고,

고유값분해가 가능하려면 행렬 A가 N개의 일차독립인 고유벡터를 가져야 한다.

 

※ 행렬 A가 일차독립이라는 말은 행렬 A의 열 벡터들 중 어느 한 벡터도 다른 벡터들의 일차결합으로 표현될 수 없다는 뜻이다.

 

2) 스펙트럼 분해(Spectral Decomposition)

- 고유값 분해에서 A가 대칭행렬인 경우이다.

- (★)대칭행렬은 항상 고유값 분해가 가능하며 직교행렬(P, orthogonal matrix)로 분해 가능한 성질을 가지고 있다.

$$  A = PDP^T = PDP^{-1} $$

$$ 직교행렬 \,\, P에 \,\, 대해 \,\,\, PP^T = I \,\,\, ( 즉, \,\, P^T = P^{-1} )$$

 

참고1) 

A가 대칭행렬이 아니라면, 고유값 분해는 할수 없고 Hessenberg Decomposion이 가능하다.

$$ A = PHP^T $$

$$ H는 \,\, Hessenberg \,\, form 이다 $$

 

A가 실수(real-value) 고유값을 가진다면 Schur Decomposition이 가능하다.

$$ A = PSP^T $$

$$ S는 \,\, Upper \,\, Triangular \,\, form 이다 $$

 

위의 Eigen, Hessenberg, Schur Decomposition는 A를 단순하게 표현 해준다는 점에서 중요하기도 하지만, 직교행렬 P가 반올림 오류를 확대하지 않기 때문에(do not magnify roundoff error) 중요하다. 

 

참고2) 

A가 M x N 행렬이라면,

(a) A와 $A^TA$는 같은 Null Space를 가진다.

(b) A와 $A^TA$는 같은 Row Space(행공간)을 가진다.

(c) $A^T$와 $A^TA$는 같은 Column Space(열공간)을 가진다.

(d) A와 $A^TA$는 같은 Rank를 가진다.

 

3) 특이값 분해(Singular Value Decomposition)

- 특이값 분해(SVD)는 스펙트럼 분해(SD)의 일반화된 형태이다.

 

어떠한 실수 행렬X (m x n, m $\geq$n)는 아래와 같이 분해가 가능하다.

$$ A = U\Lambda V^T$$

 

U 는

- (m x m 행렬) 열 직교 행렬(Column Orthonormal matrix) 이다 ($U^TU = I$)

- A의 Left Singular Vector 로 이루어진 (m x m 직교 행렬) 

- $AA^T$의 고유벡터이다.

 

$ \Lambda $ 는

- (m x n 행렬) 대각행렬이다. 원소는 행렬 X의 특이값이다.

- $\sqrt{\lambda_1}$, ... , $\sqrt{\lambda_k}$ 를 원소로 가진다. 

- $A^TA$의 고유값이다.

 

$V$ 는

- (n x n 행렬) 행 직교 행렬(Row Orthonormal matrix)이다. ($V^TV = I$)

- A의 Right Singular Vector 로 이루어진 (n x n 직교 행렬) 

- $A^TA$의 고유벡터이다.

 

Singular Value Decomposition of Matrix A

SVD 예시, 대각 행렬은 일반적으로 내림차순이다.

 

 

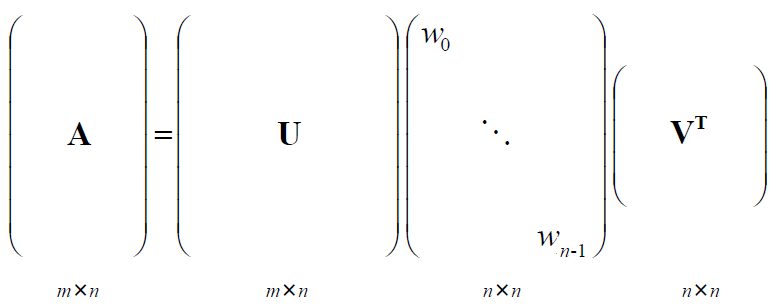
※ 행렬 분해 Diagram

 

---

출처 

[1] Howard-Anton 'Linear Algebra' 11th

[2] 박인규 교수님 강의 자료

[3] 6. Singular Value Decomposition (SVD)

[4] https://rfriend.tistory.com/185

[5] https://angeloyeo.github.io/2019/08/01/SVD.html

[6] https://darkpgmr.tistory.com/106