Q. 선형성이란 무엇인가? 1차원 직선 상의 연산은 선형성을 만족한다고 할 수 있나?
A. 아니다. 1차원 직선 상의 연산도 선형성을 만족하지 않을 수 있다. 선형성은 행렬 뿐만 아니라 함수, 연산에도 적용할 수 있는 개념이다.
(상세)
선형대수 정리에 따르면,
T: $R^n -> R^m $이 행렬 변환일 필요충분조건은, $R^n$에 있는 모든 벡터 u와 v에 대해 그리고 모든 스칼라 k에 대해 다음과 같은 관계가 성립하는 것이다.
(1) T(u + v) = T(u) + T(v) : Superposition(합의 성질)
(2) T(ku) = kT(u) : Homogeniety(동치)
위의 식을 종합하면, $T(k_{1}u + k_{2}v) = k_{1}T(u) + k_{2}T(v)$를 만족하는 것은 선형조건(Linearity Condition)을 만족한다고 할 수 있다. 이러한 조건을 만족하는 변환은 선형 변환이다.
ex1) 원점을 지나는 직선
y = mx는 선형성이 있다.
ex2) 원점을 지나지 않는 직선
y = mx + 1은 선형성이 없다.
따라서, 직선이라고 무조건 선형성을 가진다고 할 수 없다.
마찬가지로, 평면으로 확장하면 원점을 지나는 평면에 속하는 모든 벡터는 선형성을 만족하지만, 원점을 지나지 않는 평면에 속한 벡터는 선형의 성질을 만족한다고 할 수 없다.
함수가 아닌 연산(Operation)에도 선형의 개념을 적용할 수 있다.
미분(Differentiation)과 적분(Integration)은 선형의 성질을 만족한다.
선형대수 정리에 따르면,
$R^n -> R^m $으로의 모든 선형변환은 행렬변환이고, 반대로 $R^n -> R^m $로의 모든 행렬변환은 선형변환이다.
(결론)
위의 모든 내용을 종합하면, 선형조건을 만족한다면 행렬, 함수, 연산도 선형 변환이 가능하고, '행렬 변환'으로 표현할 수 있다. 예를 들어, 미분, 적분 연산은 선형성을 만족하므로 '행렬 변환'으로 표현이 가능하다.
Q. 2차원 이상 다항식을 나타내는 행렬도(아래 그림) 파라미터를 구하고자 할 때, 역행렬이 존재할 수 있는지? $ A^{-1} $ 역행렬이 존재한다면 변환행렬 A는 '선형'이라고 할 수 있는지?
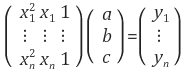
ex) f(x) = $x^2 + x - 2$, (-2, 0), (1, 0), (2,4) 로 점을 잡으면 역행렬이 존재한다.
A. 2차원 다항식 상의 점이라 할지라도 위에서 벡터는 [$x^2$, x, 1]이 아니라 아래와 같다.
$ [x_1^2, ..., x_n^2]', [x_1, ..., x_n]', [1, ..., 1]' $ 위의 벡터들은 선형 독립이다.
또한, Pseudo Inverse로 안구해도 되면 변환 행렬 A가 선형인 것이고 다항식 표현도 '선형'이 가능한가 라는 것이 질문인 것 같은데...
행벡터가 다항식으로 표현하든 안하든 상관 없이 열벡터를 기준으로 봐야한다.
$ [x_1^2, ..., x_n^2]', [x_1, ..., x_n]', [1, ..., 1]' $ 벡터들이 만든 공간(span)에 $ [y_1, ..., y_n]' $ 가 존재하므로
Pseudo Inverse로 안구해도 되는 것이다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 행렬 분해(Matrix Decomposition) 종류 (0) | 2021.07.17 |
|---|---|
| Pseudo Inverse(유사 역행렬) 및 SVD(특이값 분해)_v2 (0) | 2021.06.16 |
| 촐레스키 분해(Cholesky decomposition) (0) | 2021.04.18 |


