Triplet Loss 구현은 아래 2가지로 구성된다.
- Pair Wise Distance 계산 + Batch All Strategy 구하는 전략
- Pair Wise Distance 계산 + Batch Hard Strategy 구하는 전략
Pair Wise Distance 계산
- 임베딩 된 것 간의 거리 계산. 임베딩의 차원을 (B, 1) / (1, B)로 늘려 행렬 곱을 하면, 동일 임베딩 간의 제곱 값을 구할 수 있게 된다. tf.diag_part 참고.
- Squared 옵션을 사용하지 않는다면, '0' 값을 가진 원소를 Epsilon을 더한 후 Sqrt 연산을 진행한다.

def _pairwise_distances(embeddings, squared=False):
"""Compute the 2D matrix of distances between all the embeddings.
Args:
embeddings: tensor of shape (batch_size, embed_dim)
squared: Boolean. If true, output is the pairwise squared euclidean distance matrix.
If false, output is the pairwise euclidean distance matrix.
Returns:
pairwise_distances: tensor of shape (batch_size, batch_size)
"""
# Get the dot product between all embeddings, shape (batch_size, batch_size)
dot_product = tf.matmul(embeddings, tf.transpose(embeddings))
# Get squared L2 norm for each embedding. We can just take the diagonal of `dot_product`.
# This also provides more numerical stability (the diagonal of the result will be exactly 0).
# shape (batch_size,)
square_norm = tf.diag_part(dot_product)
# Compute the pairwise distance matrix as we have:
# ||a - b||^2 = ||a||^2 - 2 <a, b> + ||b||^2 , shape (batch_size, batch_size)
distances = tf.expand_dims(square_norm, 1) - 2.0 * dot_product + tf.expand_dims(square_norm, 0)
# Because of computation errors, some distances might be negative so we put everything >= 0.0
distances = tf.maximum(distances, 0.0)
if not squared:
# Because the gradient of sqrt is infinite when distances == 0.0 (ex: on the diagonal)
# we need to add a small epsilon where distances == 0.0
mask = tf.to_float(tf.equal(distances, 0.0))
distances = distances + mask * 1e-16
distances = tf.sqrt(distances)
# Correct the epsilon added: set the distances on the mask to be exactly 0.0
distances = distances * (1.0 - mask)
return
Batch All Strategy 구하는 전략
- 모든 배치 샘플에 대해 (Positive)와 (배치 샘플수 - Positive 갯수)를 곱해서 Triplet을 구한다.
: 한 배치당
- (B, B, B) 3차원 텐서를 구하고, 유효하지 않은 인덱스(Anchor와 Positive의 라벨이 같지 않거나, Anchor와 Negative의 라벨에 같거나, Anchor와 Positve 샘플이 정확히 일치하거나) 를 구해서 거리값 합에서 제외 시킨다.
- (1) ~ (2) 단계로 계산된다.
(1) Triplet Mask
- i, j, k 값이 모두 같지 않은 경우 즉, anchor, positive, negative 샘플은 서로 다른 상황에서
- i(anchor)와 j(positive)의 라벨은 동일하고, i(anchor)와 k(negative)의 라벨은 같지 않은 인덱스를 선택한다.
def _get_triplet_mask(labels):
"""Return a 3D mask where mask[a, p, n] is True iff the triplet (a, p, n) is valid.
A triplet (i, j, k) is valid if:
- i, j, k are distinct
- labels[i] == labels[j] and labels[i] != labels[k]
Args:
labels: tf.int32 `Tensor` with shape [batch_size]
"""
# Check that i, j and k are distinct
indices_equal = tf.cast(tf.eye(tf.shape(labels)[0]), tf.bool)
indices_not_equal = tf.logical_not(indices_equal)
i_not_equal_j = tf.expand_dims(indices_not_equal, 2)
i_not_equal_k = tf.expand_dims(indices_not_equal, 1)
j_not_equal_k = tf.expand_dims(indices_not_equal, 0)
# i, j, k 값이 모두 같지 않은 경우 즉, anchor, positive, negative 샘플은 서로 다른 상황에서
distinct_indices = tf.logical_and(tf.logical_and(i_not_equal_j, i_not_equal_k), j_not_equal_k)
# Check if labels[i] == labels[j] and labels[i] != labels[k]
label_equal = tf.equal(tf.expand_dims(labels, 0), tf.expand_dims(labels, 1))
i_equal_j = tf.expand_dims(label_equal, 2)
i_equal_k = tf.expand_dims(label_equal, 1)
valid_labels = tf.logical_and(i_equal_j, tf.logical_not(i_equal_k))
# Combine the two masks
mask = tf.logical_and(distinct_indices, valid_labels)
return mask(2) Triplet Mask X Triplet Loss
- 위에서 구한 Triplet Mask와 Triplet Loss를 행렬 곱 계산한다.
- 특이한 부분은, 유요한 Triplet 갯수 대비 Positive Triplet 비율을 같이 리턴한다.
# Get the pairwise distance matrix
pairwise_dist = _pairwise_distances(embeddings, squared=squared)
anchor_positive_dist = tf.expand_dims(pairwise_dist, 2)
anchor_negative_dist = tf.expand_dims(pairwise_dist, 1)
# Compute a 3D tensor of size (batch_size, batch_size, batch_size)
# triplet_loss[i, j, k] will contain the triplet loss of anchor=i, positive=j, negative=k
# Uses broadcasting where the 1st argument has shape (batch_size, batch_size, 1)
# and the 2nd (batch_size, 1, batch_size)
triplet_loss = anchor_positive_dist - anchor_negative_dist + margin
# Put to zero the invalid triplets
# (where label(a) != label(p) or label(n) == label(a) or a == p)
mask = _get_triplet_mask(labels)
mask = tf.to_float(mask)
triplet_loss = tf.multiply(mask, triplet_loss)
# Remove negative losses (i.e. the easy triplets)
triplet_loss = tf.maximum(triplet_loss, 0.0)
valid_triplets = tf.to_float(tf.greater(triplet_loss, 1e-16))
num_positive_triplets = tf.reduce_sum(valid_triplets) # Positive Triplet 갯수
num_valid_triplets = tf.reduce_sum(mask) # Valid Triplet 갯수
fraction_positive_triplets = num_positive_triplets / (num_valid_triplets + 1e-16)
# Get final mean triplet loss over the positive valid triplets
triplet_loss = tf.reduce_sum(triplet_loss) / (num_positive_triplets + 1e-16)
return triplet_loss, fraction_positive_triplets
Batch Hard Strategy 구하는 전략
- 한 배치 당 PK(P: 사람수, K: 사람당 이미지 수) 개의 Triplet이 생성된다.
- 아래의 (1) ~ (5) 단계로 계산된다.
(1) Anchor positive Triplet
- Anchor와 라벨은 동일하지만 인덱스는 다른 Positive를 구하는 과정. 즉, (i.e. and and have same labels)
- '인덱스가 같지 않은 것(indices_not_equal)' 은 단위 행렬의 logical_not 으로 구한다.
def _get_anchor_positive_triplet_mask(labels):
"""Return a 2D mask where mask[a, p] is True iff a and p are distinct and have same label.
Args:
labels: tf.int32 `Tensor` with shape [batch_size]
Returns:
mask: tf.bool `Tensor` with shape [batch_size, batch_size]
"""
# Check that i and j are distinct
indices_equal = tf.cast(tf.eye(tf.shape(labels)[0]), tf.bool)
indices_not_equal = tf.logical_not(indices_equal)
# Check if labels[i] == labels[j]
# Uses broadcasting where the 1st argument has shape (1, batch_size) and the 2nd (batch_size, 1)
# 라벨의 차원을 (열/행으로 각각 추가하여) 동일한 지 판별
labels_equal = tf.equal(tf.expand_dims(labels, 0), tf.expand_dims(labels, 1))
# Combine the two masks
# 다만, 동일한 인덱스는 '라벨이 당연히 동일할 것이므로' 제외한다.
mask = tf.logical_and(indices_not_equal, labels_equal)
return mask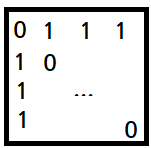
(2) Hardest Positive
- 위에서는 마스킹을 구한 과정이고, 이제 마스킹을 이용해서 거리가 가장 큰 값을 구한다.
# For each anchor, get the hardest positive
# First, we need to get a mask for every valid positive (they should have same label)
mask_anchor_positive = _get_anchor_positive_triplet_mask(labels)
mask_anchor_positive = tf.to_float(mask_anchor_positive)
# We put to 0 any element where (a, p) is not valid (valid if a != p and label(a) == label(p))
anchor_positive_dist = tf.multiply(mask_anchor_positive, pairwise_dist)
# shape (batch_size, 1)
hardest_positive_dist = tf.reduce_max(anchor_positive_dist, axis=1, keepdims=True)
tf.summary.scalar("hardest_positive_dist", tf.reduce_mean(hardest_positive_dist))
(3) Anchor Negative Triplet
- 라벨이 같지 않은 모든 인덱스 마스킹 한다.
def _get_anchor_negative_triplet_mask(labels):
"""Return a 2D mask where mask[a, n] is True iff a and n have distinct labels.
Args:
labels: tf.int32 `Tensor` with shape [batch_size]
Returns:
mask: tf.bool `Tensor` with shape [batch_size, batch_size]
"""
# Check if labels[i] != labels[k]
# Uses broadcasting where the 1st argument has shape (1, batch_size) and the 2nd (batch_size, 1)
labels_equal = tf.equal(tf.expand_dims(labels, 0), tf.expand_dims(labels, 1))
mask = tf.logical_not(labels_equal)
return
(4) Hardest Negative
- 위에서는 마스킹을 구한 과정이고, 이제 마스킹을 이용해서 거리가 가장 작은 값을 구한다.
- 이때, Anchor과 Negative는 같은 라벨이 아니어야 한다. 따라서, 여기서 트릭이 들어간다.
- 각 행에서 가장 큰 값을 'label(a)==label(n) 인 인덱스'에 더함으로서, 'label(a)==label(n) 인 인덱스'는 최소값 구할 때 선택에서 제외되게 된다.
# For each anchor, get the hardest negative
# First, we need to get a mask for every valid negative (they should have different labels)
mask_anchor_negative = _get_anchor_negative_triplet_mask(labels)
mask_anchor_negative = tf.to_float(mask_anchor_negative)
# We add the maximum value in each row to the invalid negatives (label(a) == label(n))
max_anchor_negative_dist = tf.reduce_max(pairwise_dist, axis=1, keepdims=True)
anchor_negative_dist = pairwise_dist + max_anchor_negative_dist * (1.0 - mask_anchor_negative)
# shape (batch_size,)
hardest_negative_dist = tf.reduce_min(anchor_negative_dist, axis=1, keepdims=True)
tf.summary.scalar("hardest_negative_dist", tf.reduce_mean(hardest_negative_dist))
(5) 최종 Triplet Loss 계산
# Combine biggest d(a, p) and smallest d(a, n) into final triplet loss
triplet_loss = tf.maximum(hardest_positive_dist - hardest_negative_dist + margin, 0.0)
# Get final mean triplet loss
triplet_loss = tf.reduce_mean(triplet_loss)
참고: https://omoindrot.github.io/triplet-loss#offline-and-online-triplet-mining
Triplet Loss and Online Triplet Mining in TensorFlow
Triplet loss is known to be difficult to implement, especially if you add the constraints of TensorFlow.
omoindrot.github.io
'데이터 과학 > 딥러닝(Deep Learning)' 카테고리의 다른 글
| CenterLoss의 구현 (0) | 2022.05.30 |
|---|---|
| LSTM Autoencoder 설명 (0) | 2021.05.28 |
| 공분산(Covariance) 정리 (0) | 2021.02.12 |
| PCA(주성분 분석) 정리 (0) | 2021.02.10 |
| Autoencoder 설명 (0) | 2021.02.06 |



