※ 아래는 여러 블로그를 참고하여 만든 것입니다.
사전 지식) Attention 모델
<목차>
----------------- 기본 -----------------
1) Transformer의 내부
2) Encoder의 내부
2-1) 구조
2-2) 역할
2-3) Self Attention 네트워크
3) Decoder의 내부
4) 전체 네트워크 구조
----------------- 심화 -----------------
5) Transformer 심화
5-1 ~ 6) Self-Attention 첫번째 ~ 여섯번째 단계
6) Multi-head Self Attention layers (MSA)
7) Positioning Encoding 방법
8) Decoder 상세
9) 마지막 단계
10) 학습 데이터 예시
Transfomer는 Attention을 사용하는 모델의 학습 속도를 높인다. 병렬화(Parallelization)에 이점이 있다.
※ 실제로 Google Cloud TPU 제품을 사용하기 위한 권장 모델이 Transformer 이기도 하다.
1) Transformer의 내부

- 내부 Encoder 6개 각각은 같은 네트워크 모델이지만, 가중치를 공유하지 않는다.
- Encoder와 같은 수의 Decoder가 존재한다.
- '6'이라는 숫자에 큰 의미는 없다.
2) Encoder의 내부

2-1) 구조
- Encoder 입력은 Self-Attention을 먼저 거치고, 출력이 Feed Forward NN으로 들어간다.
- Self-Attention 은 Encoder가 특정 단어를 Encoding 할때, 입력 시퀀스 상의 다른 단어(즉, 주변)를 볼수 있게 해주는 역할을 한다.
2-2) 역할
- 먼저 Embedding Algorithm에 의해 각각의 입력 단어를 벡터로 바꾸는 것으로 부터 시작한다.
- Embedding은 가장 아래 부분 Encoder에서만 일어난다.
- 모든 Encoder는(그림상에서 6개 인코더) 크기가 512인 벡터 리스트를 받는다.
- 리스트의 크기는 HyperParameter이다. 일반적으로 입력할 말 뭉치 중 가장 긴 길이를 벡터 리스트 크기로 잡는다.
- 각 단어의 위치가 Encoder의 Self Attention Layer의 자체 경로를 따라 흐른다. Self Attention안의 각 경로 끼리는 의존성이 있다(서로 독립적이지 않다)
- Feed Forward Layer에서는 각 경로 끼리 의존성은 없다. 그래서 병렬 연산이 가능하다.

※ 실제로 Encoder 내부는 자세하게 표현하면 다음과 같다.
Residual Connection(점선)이 두번 들어가고,
각각 Layer-Nomalization을 거친다.
2-3) Self Attention 네트워크

- 두 입력선이 모두 하나의 시계열 데이터로 부터 나온다.
3) Decoder의 내부

- Encoder와 공통점으로 Self-Attention 과 Feed Forward 계층이 있지만,
- 차이점으로는 Input Sentence의 관련 부분(Relevant Parts)에 집중하게 하는 계층이 있다.
(Encoder-Decoder Attention)
4) 전체 네트워크 구조

※ Encoder를 포함해서 Transfomer의 구조를 자세히 나타내면 오른쪽과 같다(Encoder를 2개만 쌓았을 경우).
Encoder의 마지막 출력 값이 Decoder 각각의 Encoder-Decoder Attention 계층으로 들어간다.
5) Transformer 심화
”The animal didn't cross the street because it was too tired” 문장을 예를 들어보자.

- 인간에게는 직관적인 문장 사이의 it의 의미가 기계가 추론할 수 있게 하려면?
- (여기서 it의 의미는 앞서 나온 명사인 'the animal'을 가리키는 것을 인간은 잘 안다)
- Self-Attention을 통해 문제 해결할 수 있다. 각 위치를 확인하여 단어를 더 잘 Encoding할 수 있는 단서를 얻는다.
- 즉, Self-Attention은 (특정) 단어가 문장내의 다른 단어를 살피며 단서를 얻어, 더 잘 인코딩 할 수 있게 한다.
(Self- Attention is the method the Transformer uses to bake the “understanding” of other relevant words into the one we’re currently processing)
※ 본인의 경우 Self-Attention을 각 단어가 주변 단어와 비교한 '자기 참조'로 이해하였다.
5-1) Self-Attention 첫번째 단계
첫번째 단계는 Encoder의 입력 벡터(e.g. Word Embedding)로 부터 3개의 벡터를 만드는 것이다
Query, Key, Value
$ q \in \mathbb{R}^d $ , d는 여기서 64
$ k \in \mathbb{R}^d $
$ v \in \mathbb{R}^d $
이 벡터들은 학습될 Matrices와의 곱을 통해 만들어 진다. 입력 벡터가 512 크기라면, 출력 벡터의 크기는 64 정도가 됨을 주목한다. (크기가 줄어든다. 항상 줄어들 필요는 없고 해당 예시가 그렇다)
Query, Key, Value는 Self-Attention Layer 계산에 등장하는 추상화된 개념으로 이해한다. 각 역할은 아래에 등장한다.
$ W \in \mathbb{R}^{n_t \times d} $ , 여기서 n_t은 512, d는 64

5-2) Self-Attention 두번째 단계
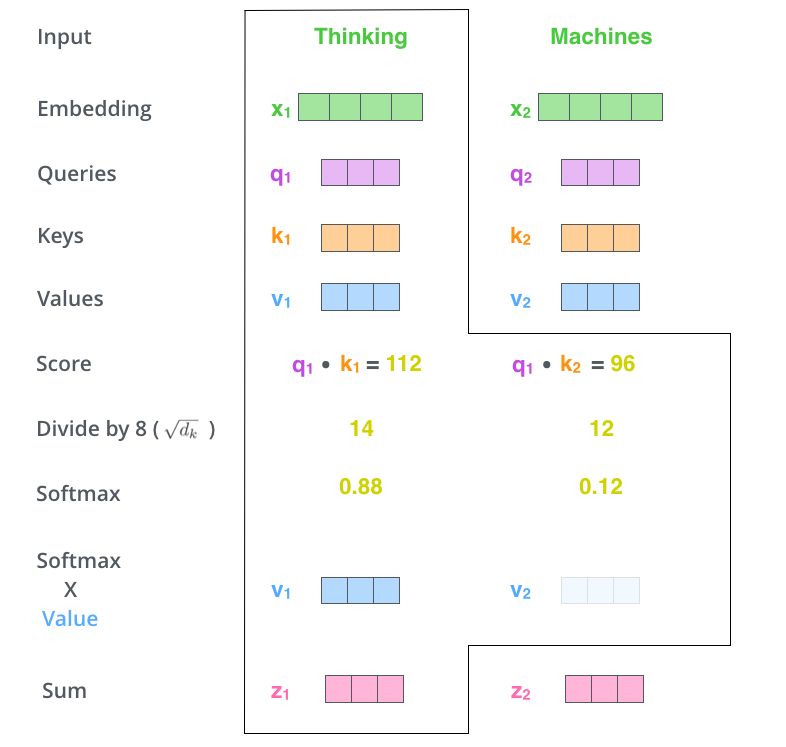
- 한 단어를 기준으로 각 단어와의 점수를 계산한다.
- 결국, 'Self-Attention'은 문장의 한 단어가, 자기 자신이 속한 문장의 다른 단어와 어떤 연관이 있는지 수치화 하는 것이다.
- 문장 중 특정 포지션의 단어를 Encode 할때, 문장의 다른 위치에 있는 부분을 얼마나 주목할 것인지 점수를 매긴다.
- Query 벡터와 각 단어의 Keys 벡터를 내적한다.
e.g. (q1 * k1), (q1 * k2), ..., (q1 * kn)
- 내적 한다는 것은 수학적으로 벡터가 얼마나 유사한 지를 수치화 하겠다는 의미이다. 연관성이 떨어질 수록 적은 값을 가진다.
5-3, 5-4) Self-Attention 세번째, 네번째 단계
- 점수를 key 벡터의 크기 제곱근($\sqrt{D} = 8$)으로 나눈다.
- 위의 나누기는 기울기 안정 효과가 있다.
- 결과를 Softmax 함수에 통과 시킨다.
- Softmax는 점수를 정규화 시킨다.
- Softmax 점수는 각각의 단어가 현재 위치에서 얼마나 표현될 지를 결정한다(?)
$$ Attention(Q, K, V) = Softmax(QK^T / \sqrt{d})V $$

5-5) Self-Attention 다섯번째 단계
- 각각의 값(Value)를 소프트맥스 점수(바로 앞단계에서 계산한 값)와 곱해준다.
- 이 연산의 의미는 집중하고자 하는 단어를 유지하고, 관련 없는 것을 사라지게 하기 위함이다.
5-6) Self-Attention 여섯번째 단계
- 가중치 값 벡터를 모두 더한다.
- 남은 Sum 벡터는 Feed-Forward 네트워크에 전달된다.
일련의 과정을 Packing하여 하나로 합칠 수 있다. 가령 단어 2개(k)를 Packing 하면 다음과 같이 된다.
(학습하는 가중치 행렬 크기는 그대로이다)

여기서 얻어진 Q, K를 다시 내적하고,
D 제곱근으로 나눈다.
그리고 Packing된 Value 벡터와 곱한다.
패킹 기법을 적용하면
$ Q \in \mathbb{R}^{N \times d} $
$ K \in \mathbb{R}^{k \times d} $
$ V \in \mathbb{R}^{k \times d} $
k = N이 되면, 입력 벡터의 단어간에 관계를
모두 고려한다는 뜻이다.

$$ Attention(Q, K, V) = Softmax(QK^T / \sqrt{d})V $$
전체 과정)
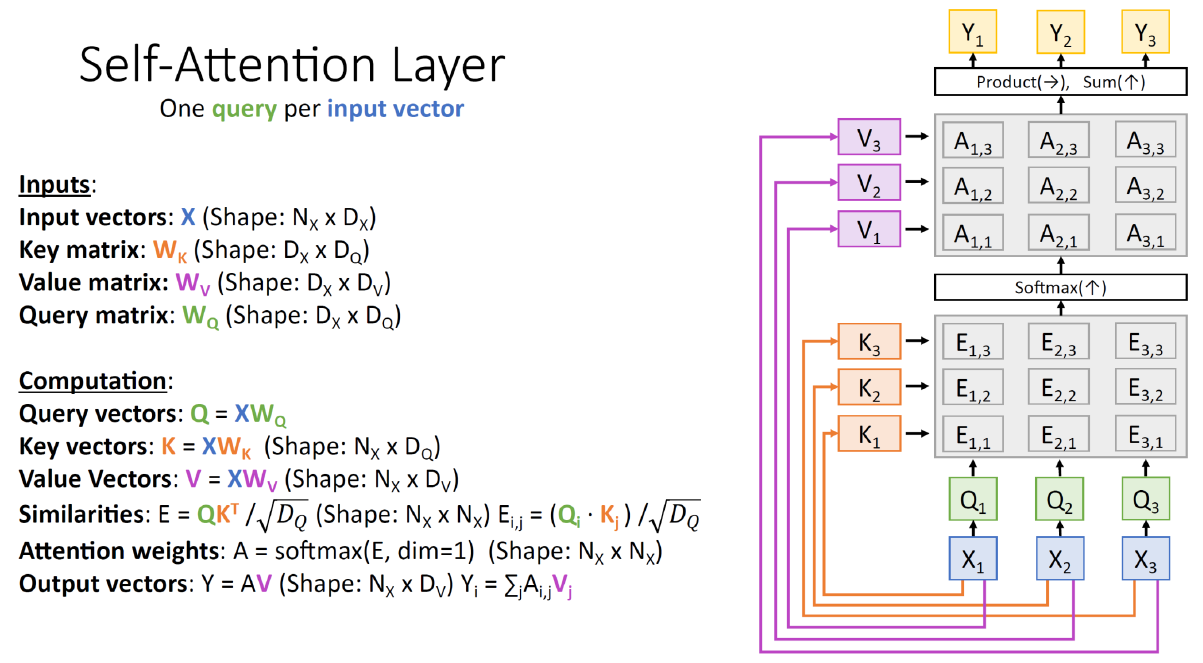
6. Multi-head Self Attention layers (MSA)
논문은 Self-Atttention을 Multi-headed로 확장 시켰다. "Multi headed" Attention은 두가지 효과가 있다.
5-1) "Multi headed"를 이용하면, 모델이 다른 위치에 집중할 수 있는 능력을 더 키울 수 있다.
5-2) "Query/Key/Value"를 다수의 집합으로 만들 수 있다(Multiple "Representation Subspaces")
- Q/K/V 행렬 표현에서 더 나아가 집합 표현으로 만들 수 있다. 예를 들어 각 인코더/디코더에 대해 8개의 세트가 만들어 질 수 있다.

Multi-headed Attention을 이용하면, 각각 Head에 Q/K/V를 분리하여 결과를 만들수 있다.

따라서, 하나의 Packing된 단어 집합에 대해 다수의 문맥 벡터 Z를 생성할 수 있다.
하지만, FeadForward Layer에는 (N x k) 사이즈의 Z 벡터만 들어갈 수 있으므로 아래와 같은 계산 트릭을 이용한다.
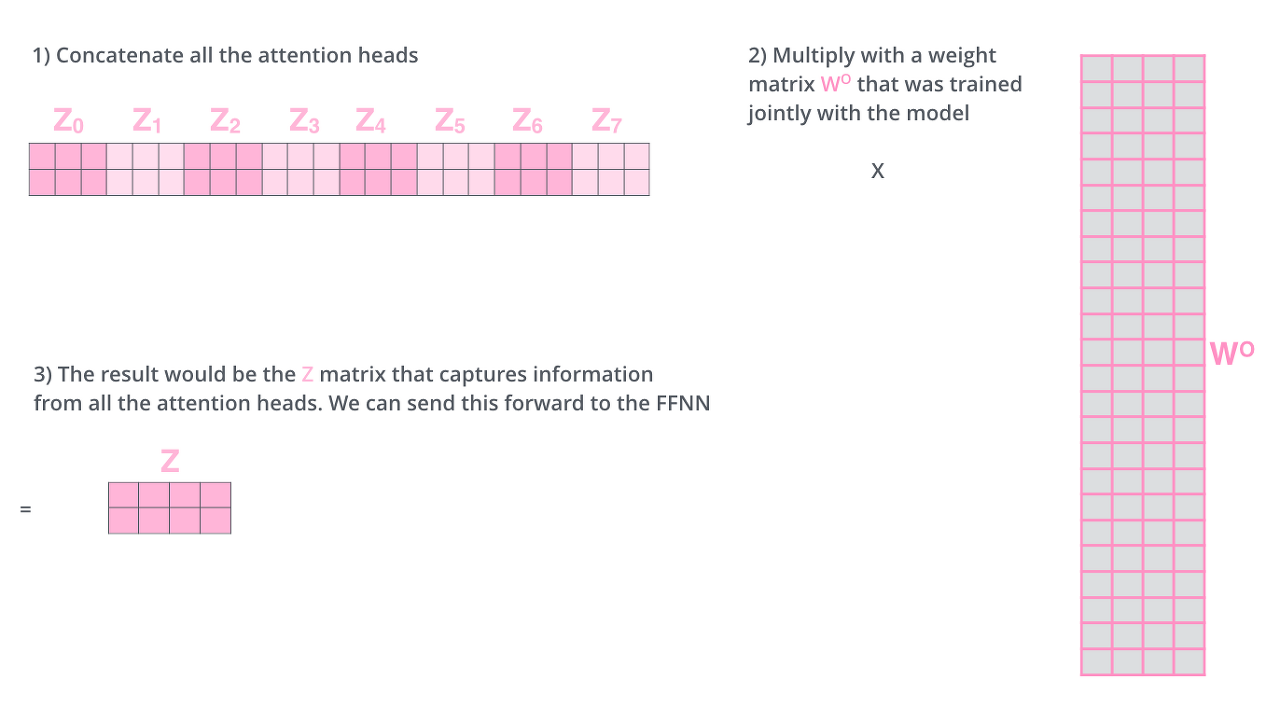
$$ \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O \\
\text{where}~\mathrm{head_i} = \mathrm{Attention}(Q, K, V) $$
Multi headed 부분을 종합하면 아래 그림과 같다.
※ 사견으로, Multi-Headed 방법은 장점 만을 결합하여 사용한다는 점에서 Ensemble 방식과 유사한 것 같다.

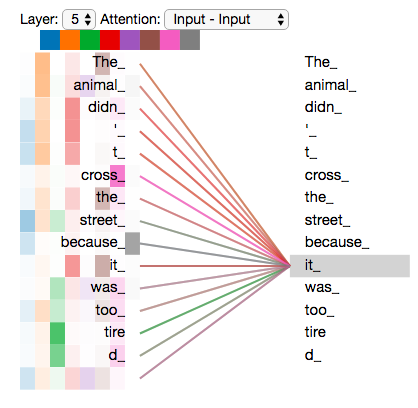
처음 예시로 다시 돌아가서, 아래는 선 색깔별로 Head가 주목하는 단어를 표현한 것이다.
- 하나의 Head는 "animal"을 주목하고, 다른 Head는 "tired"를 주목한다.
- 결국 "it"이라는 단어는 "animal"과 "tired"에 주로 연계되어 있음을 확인할 수 있다.

※ 다른 블로그의 설명
Transformer는 Multi-headed Attention을 3가지 방법으로 구성한다.
1) “Encoder-decoder attention” layers
- query는 이전 Decoder로 부터 오고, Key, Value는 Encoder 결과 값으로 부터 얻어진다.
- Decoder의 모든 위치로 하여금 Input Sequence의 모든 Position에 Attend 하게 한다
- (Seq2Seq의 문제점을 개선한 Attention의 방법과 유사한 부분 인것 같다)
2) Encoder layers
- 모든 key, value, query가 이전 Encoder 계층의 동일 위치로 부터 가져온다.
3) Decoder Layer
- leftward 방향의 정보 흐름을 막기 위해 Auto-Regression 특성을 방지해야 한다.
- 따라서, 해당 부분의 Softmax 입력을 -inf로 마스킹한다(아래 설명이 다시 나온다)
7. Positional Encoding 방법
단어의 순서를 표현하기 위하여, Positional Encoding Vector를 Embedding 벡터에 더한다.
Emedding Vector에 더하는 행위는, 각각의 임베딩 벡터(X)가 내적을 통해 Q, K, V로 각각 Projection되는 와중에 Embedding 벡터간의 '거리' 정보를 제공하게 된다.
본인의 질문)
Q. 인코더는 단어의 순서를 파악하지 못하지 때문에 Positional Encoding Vector를 더해준다고 생각하는 것이 맞는 것인가?
Q. 아래의 예시처럼 각 단어 사이 거리는 어떤 기준으로 정해지게 되는지?
Q. '더하는 행위가 내적 하는 와중에 거리 정보를 반영하게 된다'는 것이 무슨 말인지?

아래 그림에 따르면, 각 행은 벡터의 Positional Encoding에 대응된다. 첫 행은 첫번째 단어에 더하는 벡터. 각 열은 512 값을 가지고 있다 (값은 -1 ~ 1사이)
아래 예시는 20개 단어의 Positional Encoding Vector 예시이다. 중앙을 기준으로 왼쪽은 Sin 함수를 이용해서 생성된 값이고, 오른쪽은 Cosine 함수를 이용해서 생성된 것이다.


8. Decoder 상세
- 각 단계의 출력은 다음 담계의 Decoder 하단으로 공급이 된다.
- 인코더의 최 상위 출력은 K, V 벡터 세트로 변환된다. 이 벡터 세트는 "Encoder-Decoder Attention" 계층에서 사용된다.
- "Encoder-Decoder Attention"은 Decoder가 입력 시퀀스의 적절한 위치를 주목할 수 있도록 돕는다.
- 디코더에서는 인코더의 입력에서 했던 것 처럼, 각 단어의 위치를 표기하기 위해 디코더의 입력에 Positional Encoding Vector를 더한다.
- Decoder 상에서 Self-attention은 Encoder 안에 있는 것과는 약간 다르게 동작하는데, Output Sequence의 Earlier Position만 주목한다(Future Position은 -inf(무한대 음수 값)로 마스킹)
- "Encoder-Decoder Attention" 레이어는 Multi-headed self-attention 처럼 동작한다.

9) 마지막 단계
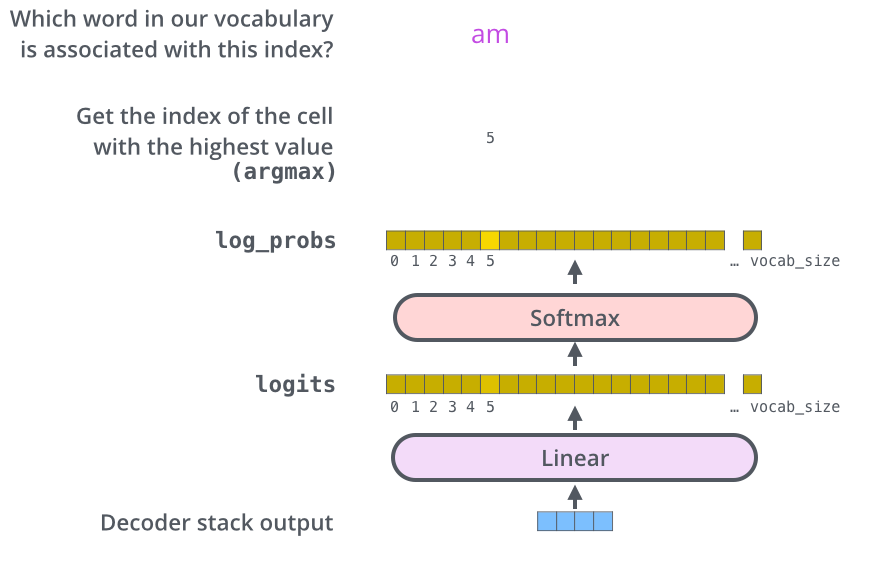
- 마지막 선형 레이어와 소프트 맥스 함수는 디코더가 출력하는 실수 벡터를 단어로 바꾸는 역햘을 한다.
- 모델이 10000개의 영단어를 알고 있다고 한다면, Logits 벡터는 10000개의 셀 너비를 가지게 된다.
각 셀은 한 단어의 점수가 된다. 소프트 맥스 함수는 각 점수를 확률로 바꿔주고, 가장 높은 점수를 가진 단어가 선택된다.
10) 학습 데이터 예시
- 출력할 단어의 갯수가 정해지고(아래 예시에서는 eos 포함 6개), 순서대로 "I am a students"를 출력해야 하기 때문에
포지션 순서대로 원핫 벡터가 Ground Truth로 주어진다.
- eos : End of Sentence
- 모델은 한 Time 동안 하나의 출력을 생산해 내고, 모델이 학습이 잘 되었다면, 각 포지션에서 가장 높은 확률의 단어를 선택하게 된다.

[Reference]
jalammar.github.io/illustrated-transformer/
nlp.seas.harvard.edu/2018/04/03/attention.html#prelims
www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained
kazemnejad.com/blog/transformer_architecture_positional_encoding/
'데이터 과학 > 딥러닝(Deep Learning)' 카테고리의 다른 글
| PCA(주성분 분석) 정리 (0) | 2021.02.10 |
|---|---|
| Autoencoder 설명 (0) | 2021.02.06 |
| Sigmoid 함수 vs Softmax 함수 (0) | 2021.02.01 |
| Attention 모델 - 구현편 (0) | 2020.12.27 |
| RNN & LSTM 설명 및 구현 (2) | 2020.11.10 |



