Chapter 6. Monte Carlo Simulation
▶ 추리 통계학
모집단(Population) : 예시들의 집합, Set of Examples.
표본(Sample) : 모집단의 적당한 부분 집합, Subset of Population.
핵심 개념 : 랜덤 샘플(random sample)한 표본은 모집단과 동일한 특성을 갖는 경향이 있음
분산이 커질 수록 같은 수준의 신뢰도를 갖기 위해서는 더 큰 표본이 필요.
▶ 큰수의 법칙(베르누이의 법칙)
각 실행에서 특정 결과가 나올 실제 확률이 p로 독립인 사건(Independent tests with the same actual probability p)에서, 실행 횟수가 무한대로 갈수록 p와 다른 결과가 나오는 횟수의 비율이 0으로 수혐한다.
▶ 도박사의 오류
서로 영향을 끼치지 않는 일련의 사건들에서 상관 관계를 찾는 오류
즉, 25번 동전이 앞면이 연속으로 나왔을 때, 26번째 던진 동전이 앞면이 나올 확률은 1/2
(왜냐하면 독립인 사건, 동전이 조작된 것이 아니라면)
▶평균으로의 회귀(Regression to the mean)
극단적인 사건 다음에 오는 사건은 덜 극단적인 경향이 있다.
e.g. 부모가 둘 다 평균 보다 키가 크면, 자식이 부모보다 작은 가능성이 높다.
부모가 평균 보다 작으면, 자식은 평균 보다 큰 가능성이 높다.
공정 룰렛 휠을 10번 돌려 빨간색이 나온다면(극단적 사례), 다음 번 10번에서는 빨간색이 10보다 적게 나온다는 개념(덜 극단적인 사례)
더 많은 표본을 취할 수록 평균에 더 가까워 진다.
def getMeanAndStd(X):
mean = sum(X)/float(len(X))
tot = 0.0
for x in X:
tot += (x - mean)**2
std = (tot/len(X))**0.5 # (tot/len(X))은 분산
return mean, std
※ 표준 편차는 평균과 같이 고려하여 생각해야 한다.
- 평균 100에 표준 편차 100 은 큰 수
- 평균 100억에서 표준 편차 100 은 작은 수
▶신뢰 구간(Confidence Interval)
값을 모르는 매개변수를 하나의 특정 값으로 설명하기 보단 신뢰 구간으로 표현하는 것이 더 좋다.
신뢰구간은 모르는 값이 포함될 가능성이 높은 구간과 그 구간에 존재할 확률을 알려준다.
e.g. 룰렛유럽 룰렛을 10k번 돌린 결과가 -3.3%이다(평균). 오차 범위는 +/- 3.5%이고 신뢰도는 95%이다(신뢰구간).
▶ 경험적인 규칙(empirical rule)을 적용하기 위한 가정(Assumption)
- 평균 추정 오차가 0이어야 한다(높게 예측할 가능성과 낮게 예측할 가능성이 같아야 한다)
- 오차 분포가 정규 분포
(해당 두 가정하에 경험적 규칙은 항상 유효하다)
--> 경험 적인 규칙은 2가지 전제하에 정규 분포를 띈다.
▶ 확률분포
- 확률 변수가 서로 다른 값을 가지는 상대적 빈도를 나타내는 개념
- 1) 이산 확률 변수
- 유한 집합의 값을 가진다. e.g. 동전의 앞 뒷면
- 2) 연속 확률 변수
- 확률 밀도 함수(PDF)를 사용

Chapter 7. Confidence Intervals
확률 밀도 함수에서 Y 축은 밀도(Density)를 뜻하며 밀도는 누적분포함수의 도함수(Cumulative Distribution Function)이다.
scipy.integrate.quad(적분할 함수, 적분 최소 한계 숫자, 적분 최대 한계 숫자, **kwargs)
- 적분하여 면적 값을 리턴한다
def gaussian(x, mu, sigma):
factor1 = (1.0/(sigma*((2*pylab.pi)**0.5)))
factor2 = pylab.e**-(((x-mu)**2)/(2*sigma**2))
return factor1*factor2
import scipy.integrate
def checkEmpirical(numTrials):
for t in range(numTrials):
mu = random.randint(-10, 10)
sigma = random.randint(1, 10)
print('For mu =', mu, 'and sigma =', sigma)
for numStd in (1, 1.96, 3):
area = scipy.integrate.quad(gaussian,
mu-numStd*sigma,
mu+numStd*sigma,
(mu, sigma))[0]
print(' Fraction within', numStd, 'std =', round(area, 4))
▶ 중심 극한 정리(Central Limit Theorem)
충분한 표본을 가지고 있다면,
1) 표본들의 평균 값(표본 평균)은 대략적으로 정규 분포.
2) 정규 분포의 평균은 모집단의 평균에 가깝다.
3) 표본 평균의 분산은 모집단의 분산을 표본의 크기로 나눈 값에 가깝다.
★모집단의 모양이 어떻든 중심 극한 정리는 성립한다(Uniform or Gaussian or Exponential 하게 분포 하던).
(모집단이 정규 분포 모양을 띄는 안띄든, 표본 평균의 분포는 정규 분포를 띈다)
##Test CLT
def plotMeans(numDice, numRolls, numBins, legend, color, style):
means = []
for i in range(numRolls//numDice):
vals = 0
for j in range(numDice):
vals += 5*random.random() # 0 ~ 5
means.append(vals/float(numDice))
pylab.hist(means, numBins, color = color, label = legend, weights = [1/len(means)]*len(means), hatch = style)
return getMeanAndStd(means)
mean, std = plotMeans(1, 1000000, 19, '1 die', 'b', '*')
print('Mean of rolling 1 die =', str(mean) + ',', 'Std =', std)
mean, std = plotMeans(50, 1000000, 19, 'Mean of 50 dice', 'r', '//')
print('Mean of rolling 50 dice =', str(mean) + ',', 'Std =', std)
pylab.title('Rolling Continuous Dice')
pylab.xlabel('Value')
pylab.ylabel('Probability')
pylab.legend()
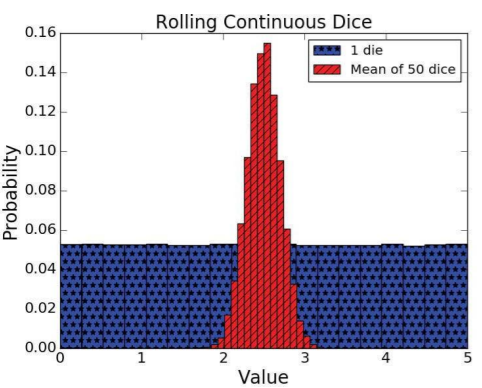
Mean of rolling 1 die = 2.498756875768418, Std = 1.4433018399078341
Mean of rolling 50 dice = 2.499870295810377, Std = 0.2029638516487054
1개의 주사위를 매우 큰 숫자 만큼 던졌을 때(1000000) 각 시행에서 숫자가 나올 확률은 거의 동일하지만,
50개의 주사위를 매우 큰 숫자 만큼 던졌을 때(1000000//50) 각 시행에서(한번 시행은 각 주사위 숫자들을 모두 더해 평균을 낸 값) 숫자가 나올 확률은 정규 분포를 띈다.
--> 주사위 1개는 표본이 작은 것이며, 주사위 50개는 표본이 충분한 것이다(중심극한정리1).
--> 주사위 1억개를 던질 경우 평균은, 주사위 50개의 평균과 거의 동일하다(중심극한정리 2).
※ 전체 시행 횟수는 동일하게 맞추기 위해 주사위 갯수로 나눈다.
Chapter 8. Sampling and Standard Error
▶추리 통계학
- 1개 이상의 임의 표본을 조사하여 모집단을 추정하는 것
- 몬테 카를로 시뮬레이션에서는 많은 표본 추출을 하여 신뢰 구간을 계산할 수 있었다.
- 시뮬레이션을 이용하지 않는다면, 어떻게 표본을 추출한 것인가??
▶확률 표본 추출
- 모집단의 모든 원소는 표본으로 선택될 확률을 가지고 있다(No bias).
- 만약 모집단이 소그룹으로 분리될 수 있다면, 단순 임의 추출(Simple random sample) 보단, 층화 추출(Stratified Sampling)을 해야 한다.
※ 층화 추출 개념 : '소집단이라 하더라도, 그들의 입장이 반영되기를 원한다'
random.sample(population, sampleSize) : 비복원 표본 추출 함수
def makeHist(data, title, xlabel, ylabel, bins = 20):
plt.hist(data, bins = bins)
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
def getHighs():
inFile = open('temperatures.csv')
population = []
for l in inFile:
try:
tempC = float(l.split(',')[1]) # 열(l)에서 두번째 원소만 취득
population.append(tempC)
except:
continue
return population
def getMeansAndSDs(population, sample, verbose = False):
popMean = sum(population)/len(population)
sampleMean = sum(sample)/len(sample)
#print('popMean :', popMean, 'sampleMean :', sampleMean)
if verbose:
print('Population mean =', popMean)
print('Standard deviation of population =', numpy.std(population))
print('Sample mean =', sampleMean)
print('Standard deviation of sample =', numpy.std(sample))
makeHist(population,
'Daily High 1961-2015, Population\n' +\
'(mean = ' + str(round(popMean, 2)) + ')',
'Degrees C', 'Number Days')
plt.figure()
makeHist(sample, 'Daily High 1961-2015, Sample\n' +\
'(mean = ' + str(round(sampleMean, 2)) + ')',
'Degrees C', 'Number Days')
plt.show()
return popMean, sampleMean, numpy.std(population), numpy.std(sample)
random.seed(0)
population = getHighs()
sampleSize = 1000
numSamples = 100
sampleMeans = []
for i in range(numSamples):
sample = random.sample(population, sampleSize)
popMean, sampleMean, popSD, sampleSD = getMeansAndSDs(population, sample, verbose = False)
sampleMeans.append(sampleMean)
print('Mean of sample Means =', round(sum(sampleMeans)/len(sampleMeans), 3))
print('Standard deviation of sample means =', round(numpy.std(sampleMeans), 3))
makeHist(sampleMeans, 'Means of Samples', 'Mean', 'Frequency')
plt.axvline(x=popMean, color ='r')
plt.show()
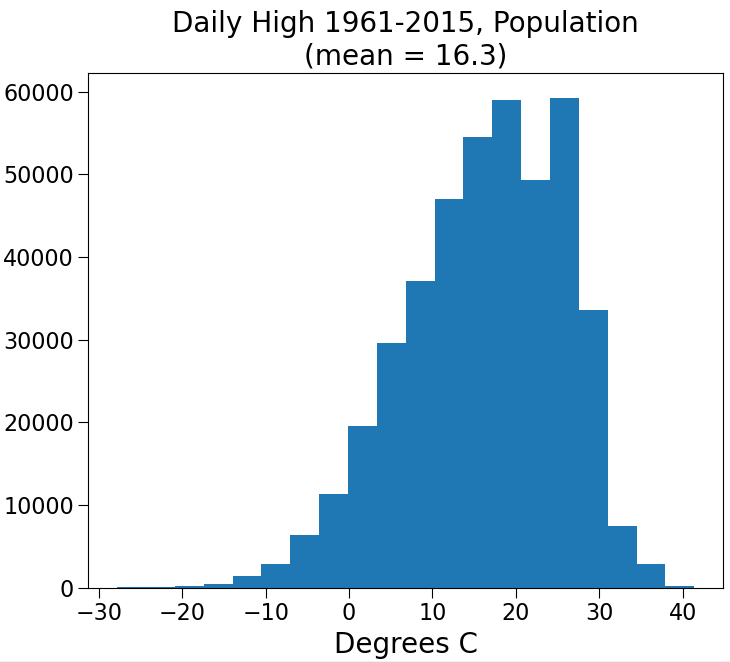
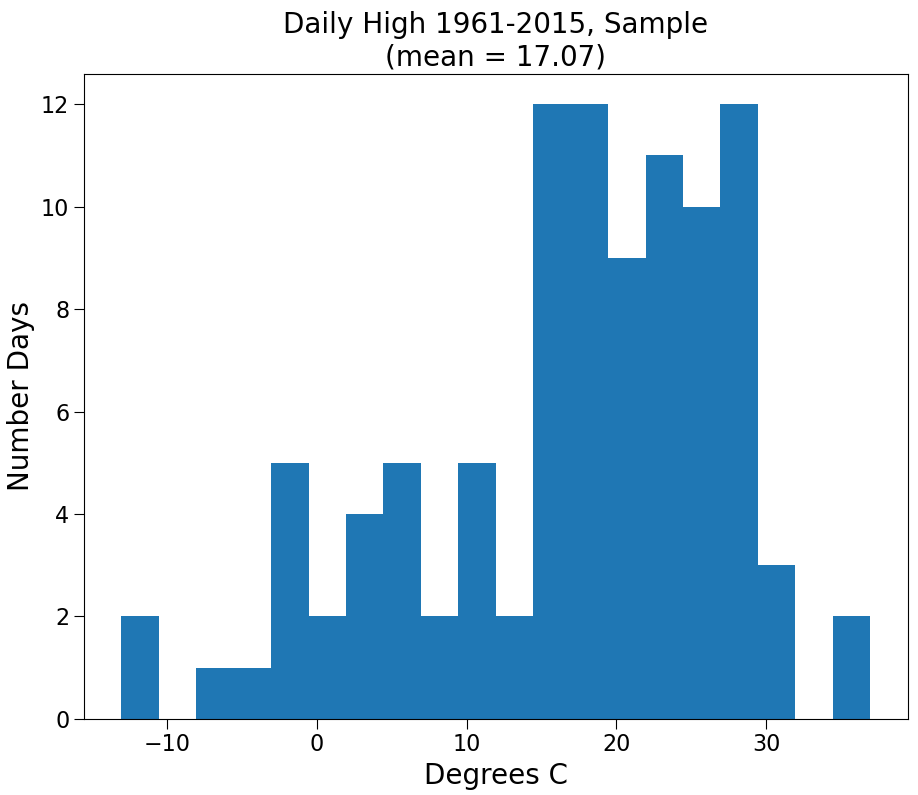
Population mean = 16.298769461986048
Standard deviation of population = 9.437558544803602
Sample mean = 17.0685
Standard deviation of sample = 10.390314372048614
모집단과 표본의 분포는 유사하며 평균과 표준 편차도 유사하다. 우연이라고 할 수 있을까??
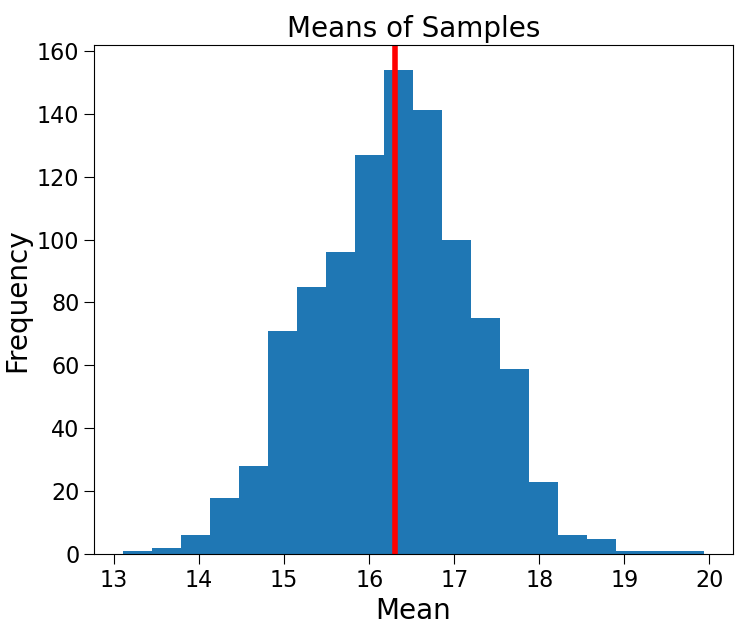
Mean of sample Means = 16.294
Standard deviation of sample means = 0.943
표본 추출(100개)를 1000번 진행해서 평균을 내 보았다.
(정규 분포 모양을 띄는 것으로 보아, 100개의 표본은 충분한 것으로 판단 됨)
하지만, 분포가 너무 넓다. 즉, 임의 표본이 모집단의 특성을 더 잘 반영하고 싶다면 어떻게 해야 할까??
- 표본 추출 횟수를 늘려야 할까? : No. 종 모양이 더 완전해질 뿐이다.
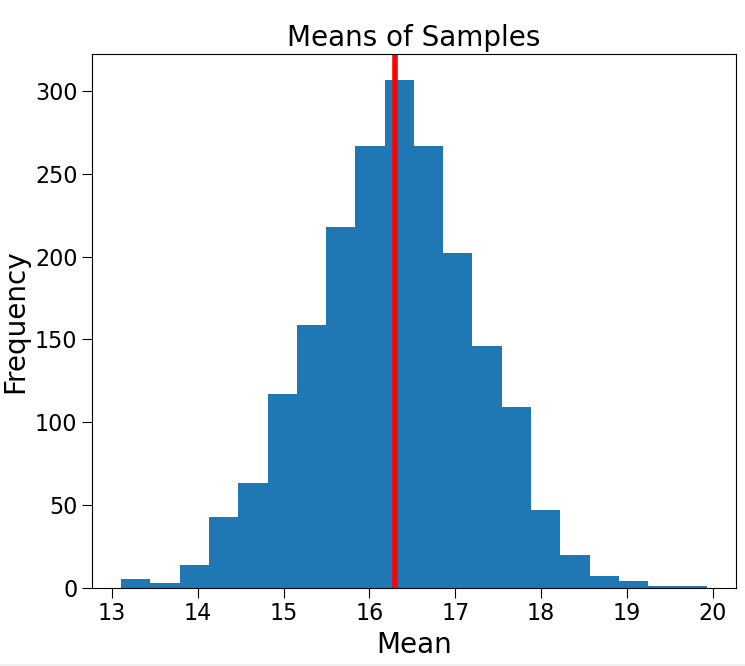
Mean of sample Means = 16.282
Standard deviation of sample means = 0.946
- 표본의 크기를 늘려야 할까? : Yes. 모집단의 특성을 더 잘 반영한다.
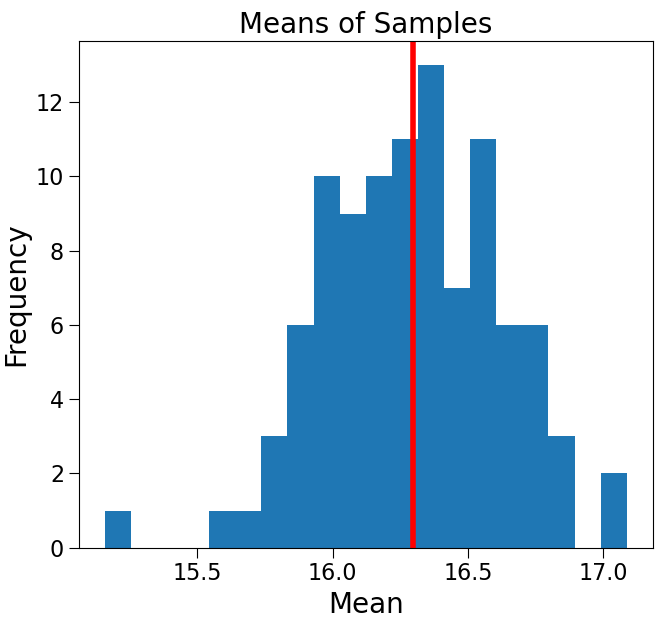
Mean of sample Means = 16.295
Standard deviation of sample means = 0.326
표본 평균( $\bar{X_i}$ )이 새로운 확률 변수(Random Variable)가 되어서 다음과 같이 분석할 수 있다.
임의 표본 평균 : $ \bar{X_i} $
표본 평균의 평균(Mean of sampling mean) :
$$ E[\bar{X}] = {1 \over n}(\bar{X_1} + ... +\bar{X_n})$$
표본 평균의 분산(Variance of sampling mean) :
$$ Var[\bar{X}] = { \sum_{i=1}^{n}(\bar{X}_i - E[\bar{X}])^2 \over n-1 } $$
표본 평균의 표준 편차(Standard deviation of sampling mean) :
$$ \sqrt{Var[\bar{X}]} $$
※ ↑타 블로그와 수식표기법에 차이가 있을 수 있습니다.
def showErrorBars(population, sizes, numTrials):
xVals = []
sizeMeans, sizeSDs = [], []
for sampleSize in sizes: # 표본의 크기
xVals.append(sampleSize)
trialMeans = [] # 표본의 크기에 따른 표본 평균
for t in range(numTrials):
sample = random.sample(population, sampleSize)
popMean, sampleMean, popSD, sampleSD = getMeansAndSDs(population, sample)
trialMeans.append(sampleMean)
sizeMeans.append(sum(trialMeans)/len(trialMeans)) # 표본 평균의 '평균'
sizeSDs.append(numpy.std(trialMeans)) # 표본 평균의 '표준 편차'
#print(sizeSDs)
plt.errorbar(xVals, sizeMeans,
yerr = 1.96*numpy.array(sizeSDs), fmt = 'o',
label = '95% Confidence Interval')
plt.title('Mean Temperature (' + str(numTrials) + ' trials)')
plt.xlabel('Sample Size')
plt.ylabel('Mean')
plt.axhline(y=popMean, color ='r', label = 'Population Mean') #모집단의 평균
plt.xlim(0, sizes[-1] + 10)
plt.legend()
plt.show()
random.seed(0)
population = getHighs()
showErrorBars(population, (50, 100, 200, 300, 400, 500, 600), 100)
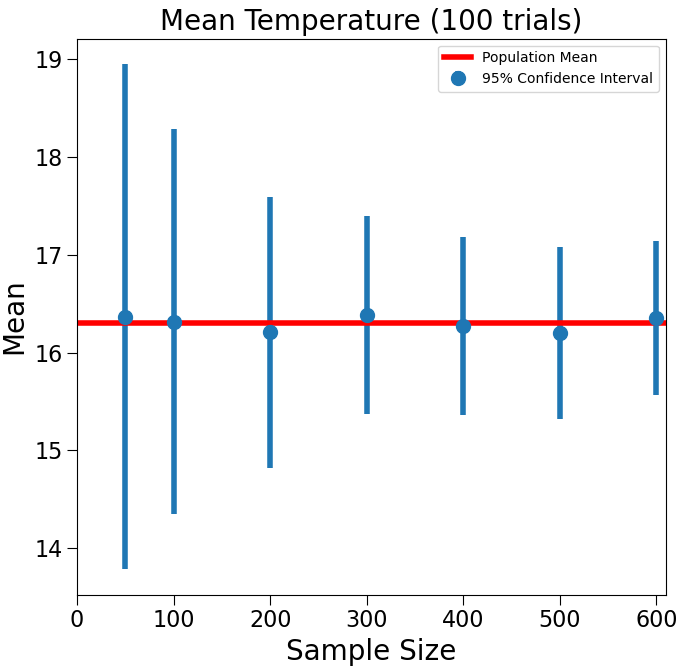
표본의 크기가 작으면 표준 편차가 큰 것을 볼수 있고(즉, 표본의 평균이 왔다갔다 한다는 것이고),
표본의 크기가 크면 표준 편차가 작은 것을 볼 수 있다(즉, N이 충분히 클때 어느 N을 모집단으로 부터 수집해도 평균이 균일하다는 것을 뜻한다).
결론 : 충분히 큰 크기의 표본으로 얻은 평균과 표준 편차는 모집단의 특성을 유사하게 반영한다고 할 수있다.
▶ 평균의 표준 오차(Standard Error of Mean, SEM)
- 표준 오차(SE)로도 부른다
- SEM: $$ {\sigma \over \sqrt{n}} $$
- 모집단의 표준 편차를 표본 크기의 제곱근으로 나눈 값
이때 모집단의 표준 편차($\sigma$)를 구하기가 어렵다면 ??
def sem(popSD, sampleSize):
return popSD/sampleSize**0.5
sampleSizes = (25, 50, 100, 200, 300, 400, 500, 600)
numTrials = 50
population = getHighs()
popSD = numpy.std(population) # 모집단의 표준편차
sems = []
sampleSDs = []
for size in sampleSizes:
sems.append(sem(popSD, size)) # 모집단의 표준 편차를 표본의 제곱근으로 나눈 것
means = []
for t in range(numTrials):
sample = random.sample(population, size)
means.append(sum(sample)/len(sample))
sampleSDs.append(numpy.std(means)) # 표본 평균의 표준편차
plt.plot(sampleSizes, sampleSDs, label = 'Std of ' + str(numTrials) + ' means')
plt.plot(sampleSizes, sems, 'r--', label = 'SEM')
plt.xlabel('Sample Size')
plt.ylabel('Std and SEM')
plt.title('SD for ' + str(numTrials) + ' Means and SEM')
plt.legend()
plt.show()
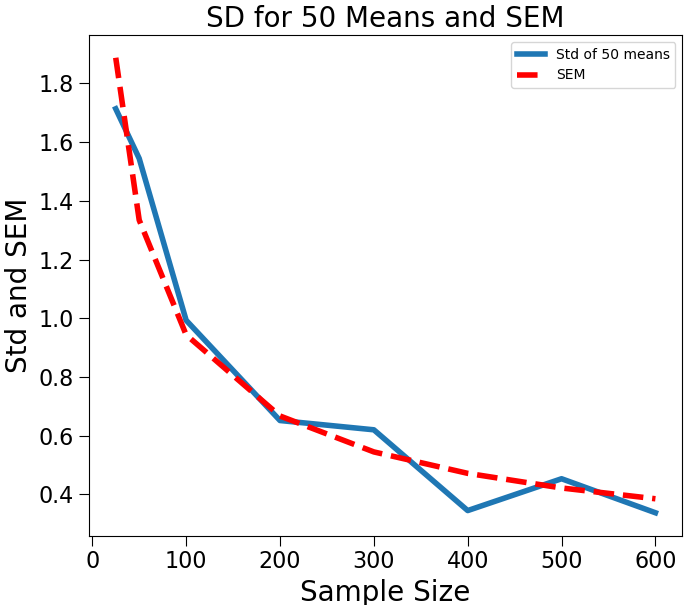
'표본 평균의 표준편차'와 '표준오차'는 근사한다.
심지어 표본의 크기가 커질 수록 더욱 가까워 진다.
모집단의 표준 편차를 구하기 어려워 SEM을 계산하기 힘들다면, 표본 평균의 표준편차로 대신한다.
(↓지금 부터는 하나의 표본에 관한 이야기 이다)
▶ 표본 표준편차과 모집단의 표준편차와의 차이
- 표본 평균의 표준편차($ Std(\bar{X}) $이 아닌, 표본의 표준편차($ Std(X_i)$) 임에 주의
def getDiffs(population, sampleSizes):
popStd = numpy.std(population)
diffsFracs = []
for sampleSize in sampleSizes:
diffs = []
for t in range(100): # 100회 시도
sample = random.sample(population, sampleSize)
diffs.append(abs(popStd - numpy.std(sample))) # 모집단 표준 편차 - 표본 표준 편차(표본 평균의 표준 편차 아니다)
diffMean = sum(diffs)/len(diffs) # 차이의 평균
diffsFracs.append(diffMean/popStd) # 차이 평균을 모집단의 표준 편차로 나눈 것
return numpy.array(diffsFracs)*100
def plotDiffs(sampleSizes, diffs, title, label, color = 'b'):
plt.plot(sampleSizes, diffs, label = label,
color = color)
plt.xlabel('Sample Size')
plt.ylabel('% Difference in SD')
plt.title(title)
plt.legend()
#plt.show()
sampleSizes = range(20, 600, 1)
diffs = getDiffs(getHighs(), sampleSizes)
plotDiffs(sampleSizes, diffs, 'Sample SD vs Population SD, Temperatures', label = 'High temps')
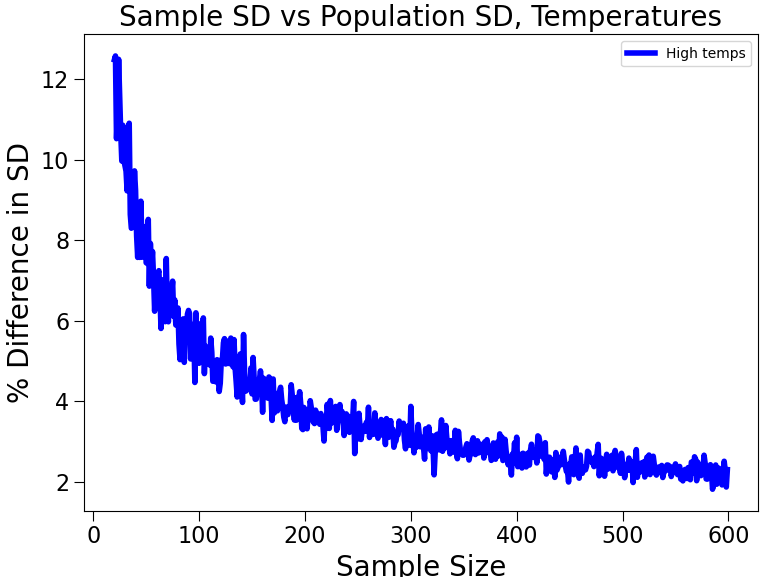
표본의 크기가 클 수록 표본 표준편차(혹은 분산)은 모집단의 표준편차(혹은 분산)에 가까워 진다.
즉, 하나의 표본만 있어도 크기가 충분히 크다면 모집단의 특성을 반영할 수 있다는 뜻이다.
※ (주의) 표본 평균의 분산이 아닌, 표본 분산이다.
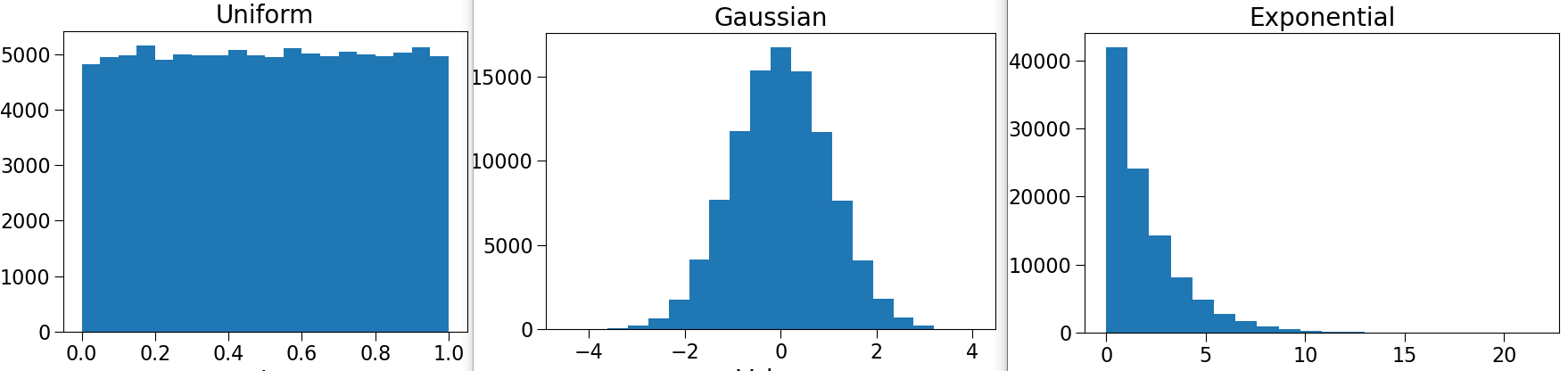
▶ 모집단의 분포가 정규 분포를 따르지 않는 경우
- 모집단의 분포가 정규 분포를 따르지 않아도 하나의 표본이 모집단의 특성을 반영할 수 있을 것인가
def compareDists():
uniform, normal, exp = [], [], []
for i in range(100000):
uniform.append(random.random()) # 모집단을 새로 생성1
normal.append(random.gauss(0, 1)) # 모집단을 새로 생성2
exp.append(random.expovariate(0.5)) # 모집단을 새로 생성3
sampleSizes = range(20, 600, 1)
udiffs = getDiffs(uniform, sampleSizes)
ndiffs = getDiffs(normal, sampleSizes)
ediffs = getDiffs(exp, sampleSizes)
plotDiffs(sampleSizes, udiffs,
'Sample SD vs Population SD', 'Uniform population', 'm')
plotDiffs(sampleSizes, ndiffs,
'Sample SD vs Population SD', 'Normal population', 'b')
plotDiffs(sampleSizes, ediffs,
'Sample SD vs Population SD', 'Exponential population', 'r')
plt.show()
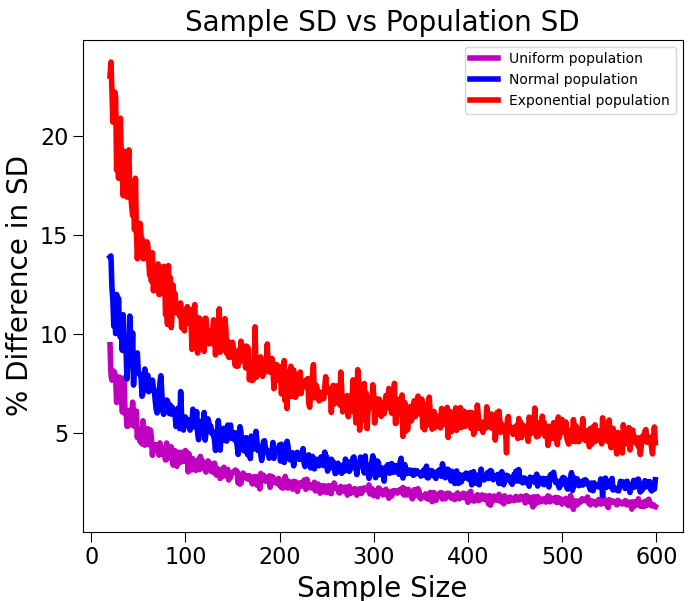
꼭 그렇지만은 않다. 표본의 크기가 커야하겠지만, 표본의 크기가 작으면은 모집단의 특성을 표본이 반영한다고 말할 수 없다.
전문 용어로 왜도(skewness, 분포의 비대칭도) 때문.
▶ 표본의 크기를 정하는 방법
- 모집단의 왜도에 따라 표본의 크기를 결정한다.
- 왜도가 클 수록 좋은 근사치를 얻기 위해 더 많은 표본이 필요하다(자세한건 링크 참조)
- 지금껏 표본 평균의 표준 편차로 표준오차(SEM)을 근사하였다면, 하나의 표본의 표준 편차로 표준오차를 근사할 수 있다.
전체 과정
1. 모집단(Population)의 왜도(Skewness) 추정값에 따라 표본의 크기(Size of sample) 결정
2. 모집단으로부터 임의 표본 추출(Ramdom Sample)
3. 표본의 평균과 표준편차 계산(Mean, Std)
4. 표본의 표준편차를 이용해 표준오차 추정(SE)
5. 표준오차 추정값을 통해 표본평균 주변의 신뢰구간 생성(Confidence Interval)
Chapter 9. Understanding Experimental Data (cont.)
▶ 계수추정
- 다항식 곡선 피팅
- numpy의 polyfit 함수를 이용한다.
- 목적함수를 최소화 하기 위해, 선형 회귀를 이용해 다항식을 표현한다.
'''
numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False) # 계수 추정 Least squares polynomial fit.
numpy.polyval(p, x) # 다항식 생성 Evaluate a polynomial at specific values.
If p is of length N, this function returns the value: p[0]*x**(N-1) + p[1]*x**(N-2) + ... + p[N-2]*x + p[N-1]
'''
def getData(fileName):
dataFile = open(fileName, 'r')
distances = []
masses = []
dataFile.readline() #discard header
for line in dataFile:
d, m = line.split()
distances.append(float(d)) #left
masses.append(float(m)) #right
dataFile.close()
return (masses, distances)
def fitData(fileName):
xVals, yVals = getData(fileName)
xVals = numpy.array(xVals)
yVals = numpy.array(yVals)
xVals = xVals*9.81 #get force
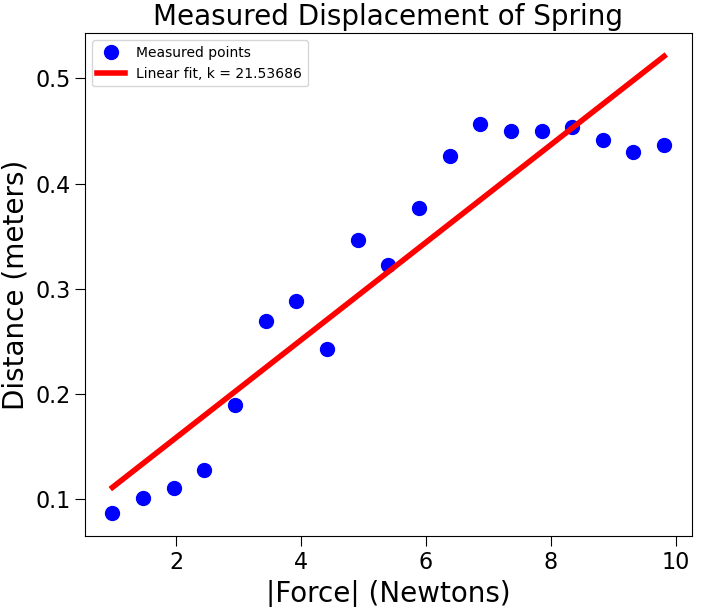
plt.plot(xVals, yVals, 'bo', label = 'Measured points')
labelPlot()
a,b = numpy.polyfit(xVals, yVals, 1) # 계수 추정
estYVals = a*numpy.array(xVals) + b
print('a =', a, 'b =', b) # 기울기와 y 절편
plt.plot(xVals, estYVals, 'r', label = 'Linear fit, k = '
+ str(round(1/a, 5)))
plt.legend(loc = 'best')
plt.show()
#fitData('springData.txt')
# polyval 이용 할 경우
def fitData1(fileName):
xVals, yVals = getData(fileName)
xVals = pylab.array(xVals)
yVals = pylab.array(yVals)
xVals = xVals*9.81 #get force
plt.plot(xVals, yVals, 'bo', label = 'Measured points')
labelPlot()
model = pylab.polyfit(xVals, yVals, 1) # 혹은 다항식을 계산
estYVals = numpy.polyval(model, xVals)
plt.plot(xVals, estYVals, 'r', label = 'Linear fit, k = '
+ str(round(1/model[0], 5)))
plt.legend(loc = 'best')
plt.show()
#fitData1('springData.txt')
'''
<'springData.txt'>
Distance (m) 0.0865 0.1015 0.1106 0.1279 0.1892 0.2695 0.2888 0.2425 0.3465 0.3225 0.3764 0.4263 0.4562 0.4502 0.4499 0.4534 0.4416 0.4304 0.437
Mass (kg) 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0
'''
def rSquared(observed, predicted):
error = ((predicted - observed)**2).sum()
meanError = error/len(observed)
return 1 - (meanError/numpy.var(observed))
def genFits(xVals, yVals, degrees):
models = []
for d in degrees:
model = pylab.polyfit(xVals, yVals, d)
models.append(model)
return models #계수 반환
def testFits(models, degrees, xVals, yVals, title):
pylab.plot(xVals, yVals, 'o', label = 'Data')
for i in range(len(models)):
estYVals = pylab.polyval(models[i], xVals)
error = rSquared(yVals, estYVals)
pylab.plot(xVals, estYVals,
label='Fit of degree ' + str(degrees[i])\
+ ', R2 = ' + str(round(error, 5)))
pylab.legend(loc = 'best')
pylab.title(title)
pylab.show()
xVals, yVals = getData('mysteryData.txt')
degrees = (1, 2)
models = genFits(xVals, yVals, degrees)
testFits(models, degrees, xVals, yVals, 'Mystery Data')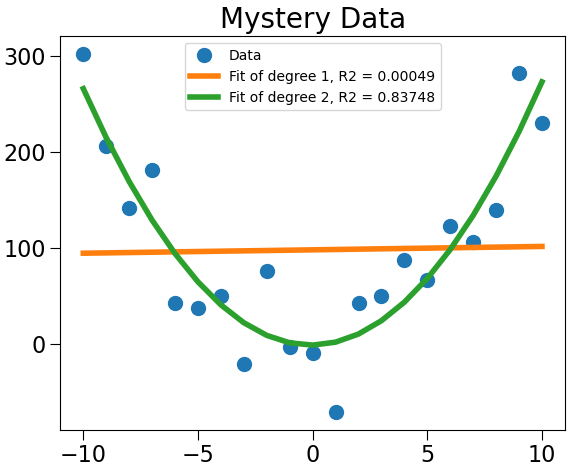
▶ 결정계수($R^2$)
- 추정한 선형 모델이 주어진 자료에 적합한 정도를 재는척도.
- 결정계수가 0에 가까우면, 회귀 모형은 유용성이 낮고, 1에 가까우면 유용성이 높다.
- 수식 : (제곱 오차들의 합) / (관측 값의 분산)
$$ R^2 = 1 - { \sum_{i}(y_i - p_i)^2 \over \sum_{i}(y_i - \mu)^2} $$
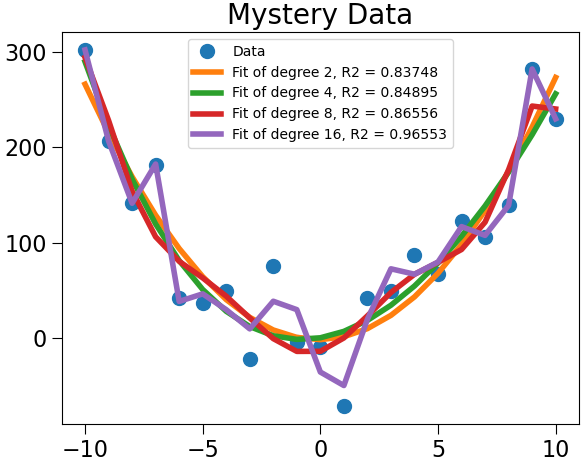
다항식 지수를 높여, 결정계수를 높일 수 있지만, 오버 피팅의 위험이 있다.
Chapter 10. Understanding Experimental Data (cont.)
def genNoisyParabolicData(a, b, c, xVals, fName):
yVals = []
for x in xVals:
theoreticalVal = a*x**2 + b*x + c
yVals.append(theoreticalVal + random.gauss(0, 35))
f = open(fName,'w')
f.write('y x\n')
for i in range(len(yVals)):
f.write(str(yVals[i]) + ' ' + str(xVals[i]) + '\n')
f.close()
#parameters for generating data
xVals = range(-10, 11, 1)
a, b, c = 3.0, 0.0, 0.0 # 계수
degrees = (2, 4, 8, 16)
#generate data
random.seed(0)
genNoisyParabolicData(a, b, c, xVals,'Dataset 1.txt') # 데이터 생성
genNoisyParabolicData(a, b, c, xVals,'Dataset 2.txt') # 데이터 생성
xVals1, yVals1 = getData('Dataset 1.txt')
models1 = genFits(xVals1, yVals1, degrees)
testFits(models1, degrees, xVals1, yVals1,'DataSet 1.txt')
pylab.figure()
xVals2, yVals2 = getData('Dataset 2.txt')
models2 = genFits(xVals2, yVals2, degrees)
testFits(models2, degrees, xVals2, yVals2,'DataSet 2.txt')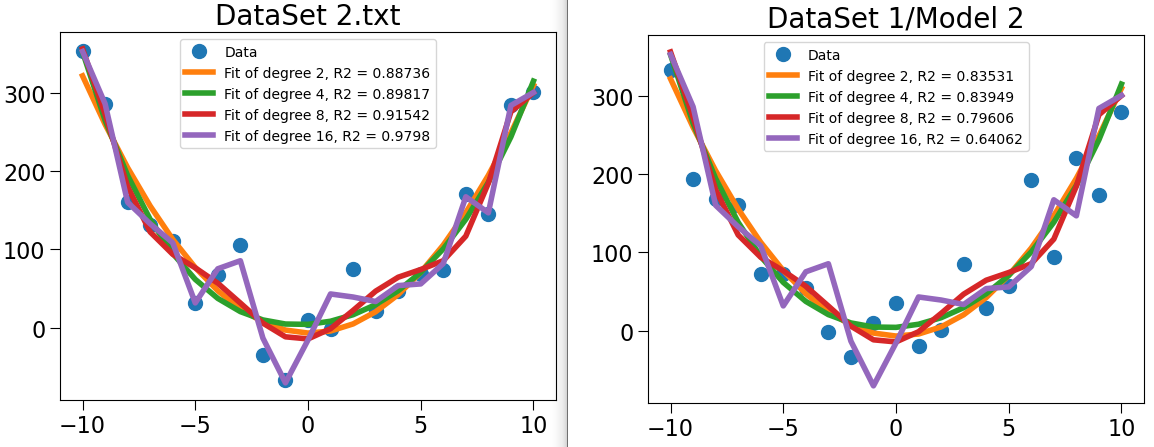
DatsSet2에 결정 계수가 높은 모델이, Dataset1에서는 결정 계수가 낮은 것을 볼 수 있다. 즉, 특정 데이터에 오버피팅(Overfitting)되어 있다. 따라서 4차원 다항식 모델이 Dataset1, 2 모두에 잘 맞는 준수한 모델이라고 할 수 있다.
'데이터 과학 > 데이터 과학' 카테고리의 다른 글
| KL Divergence(Kullback Leibler Divergence) 설명 (0) | 2021.11.01 |
|---|---|
| Density Estimation (in Python) (0) | 2021.03.26 |
| [MIT] 데이터 사이언스 기초 강의 요약[11 ~ 15강] (0) | 2020.11.29 |
| JSON (JavaScript Object Notation) in C (0) | 2020.11.09 |
| [MIT] 데이터 사이언스 기초 강의 요약[1 ~ 5강] (0) | 2020.08.28 |


