Chapter 1, 2. Optimization Problems
탐욕 알고리즘
- 순간에 최적이라고 생각하는 것을 선택해 나간다.
장점 : 구현이 쉬움, 빠르다
단점 : 최적의 해가 아닐 수도 있다.
Brute Force 알고리즘
- 항목 전체 조합을 나열하여 한계를 벗어나는 것은 제거.
동적 프로그래밍
- 복잡한 문제를 간단한 여러 개의 문제로 나누어 해결.
- 동적 프로그래밍의 알고리즘인 'memoization'을 적용하려면 참조적 투명성(referential transparency)가 보장되어야 한다.
※ 참조적 투명성(referential transparency) : 입력이 같으면, 출력이 동일. 함수 반환값이 입력값 만으로 결정된다.
def fastFib(n, memo = {}):
"""Assumes n is an int >= 0, memo used only by recursive calls
Returns Fibonacci of n"""
if n == 0 or n == 1:
return 1
try:
return memo[n]
except KeyError:
result = fastFib(n-1, memo) + fastFib(n-2, memo)
memo[n] = result
return result
for i in range(121):
print('fib(' + str(i) + ') =', fastFib(i))
정리
1. 실용적으로 중요한 문제는 최적화 문제로 바꿀 수 있다.
2. 그리디 알고리즘은 때론 적합한 하지만 최적화 되지 않은(adequate though not necessarily optimal) 해답을 제공한다
3. 최적화 된 답을 찾는 것은 종종 기하 급수적인 경우가 많아 찾기 힘들다(exponetially hard)
4. 하지만, 동적 프로그래밍을 이용하면 항상 최적의 해를 찾아주고 매우 빠르다.
Chapter 3. Graph-theoretic Models
학습 목표
- 계산 모델의 생성
- 계산 모델의 일종인 그래프를 이해한다
- 그래프에서의 최적화 알고리즘을 이해한다
※ 계산 모델 : 복잡한 현상이나 시스템을 컴퓨터를 이용해 풀기 위해 설계한 모델
※ 세상은 거대한 네트워크로 이루어져 있어, 이러한 관계는 그래프로 표현하기 적합하다.
(추상화를 통해 불필요한 정보는 버린다)
※ 그래프는 유방향 그래프(Digraph)의 서브 클래스이다.
class Graph(Digraph):
def addEdge(self, edge):
Digraph.addEdge(self, edge)
rev = Edge(edge.getDestination(), edge.getSource())
Digraph.addEdge(self, rev)
DFS(Depth Firch Search) : 깊이 우선 탐색, O(|V| + |E|)
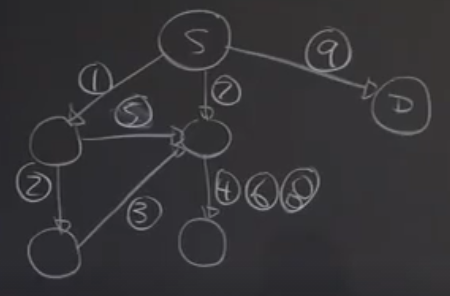
def DFS(graph, start, end, path, shortest, toPrint = False):
"""Assumes graph is a Digraph; start and end are nodes;
path and shortest are lists of nodes
Returns a shortest path from start to end in graph"""
path = path + [start]
if toPrint:
print('Current DFS path:', printPath(path))
if start == end:
return path
for node in graph.childrenOf(start):
if node not in path: #avoid cycles
if shortest == None or len(path) < len(shortest):
newPath = DFS(graph, node, end, path, shortest, toPrint)
if newPath != None:
shortest = newPath
elif toPrint:
print('Already visited', node)
return shortest
BFS(Breadth-First Search) : 너비 우선 탐색, O(|V| + |E|)
- 큐에 모든 노드를 Push/Pop : O(|V|)
- 노드의 모든 엣지를 스캔 : O(|E|)
(..BFS 코드는 생략..)
Chapter 4. Stochastic Thinking
import random
def rollDie():
"""returns a random int between 1 and 6"""
return random.choice([1,2,3,4,5,6])
def runSim(goal, numTrials, txt):
total = 0
for i in range(numTrials):
result = ''
for j in range(len(goal)):
result += str(rollDie())
if result == goal: # 1000번 시도 11111이 나올 확률
total += 1
print('Actual probability of', txt, '=',round(1/(6**len(goal)), 8)) # 6의 N승
estProbability = round(total/numTrials, 8)
print('Estimated Probability of', txt, '=', round(estProbability, 8))
runSim('11111', 10000000, '11111')
'''
Actual probability of 11111 = 0.0001286
Estimated Probability of 11111 = 0.0001286 #시행 횟수를 늘릴수록 추정 값에 더 근사해진다.
'''
runSim('11111', 100000, '11111')
'''
Actual probability of 11111 = 0.0001286
Estimated Probability of 11111 = 0.00017
'''시행횟수(numTrials)를 늘리면, 추정 확률 값(Estimatied Probability)이, 실제 확률 값(Actual Probability)에 가까워 진다.
추정 확률 값과 실제 확률 값을 혼동하면 안된다.
충분한 시도 횟수(numTrials)가 얼마 만큼인지는 이후에 다루게 된다.
※ 의사(Pseudo) 난수 생성기 함수
'''
random.seed(a=None, version=2)
- a가 None이 되면, 현재 시스템 시간이 사용된다.
- 시드(a)가 동일하다면, 동일한 난수를 발생시키게 된다
(경우에 따라 동일한 순서의 난수가 필요한 경우가 있다)
'''
import random
random.seed(100)
random.random() # 0.1456692551041303
random.random() # 0.2661737230725406
random.seed(100)
random.random() # 0.1456692551041303
random.random() # 0.45492700451402135
Birthday Problem
- 그룹([10, 20, 40, 100])에서 생일이 같은 사람이 있는 확률
def sameDate(numPeople, numSame):
possibleDates = range(366)
birthdays = [0]*366
for p in range(numPeople):
birthDate = random.choice(possibleDates) # 366일중 생일 임의로 선택
birthdays[birthDate] += 1 # 카운트 증가
return max(birthdays) >= numSame # 생일이 중복되는 사람이 발생
def birthdayProb(numPeople, numSame, numTrials):
numHits = 0
for _ in range(numTrials): # 10000번 시도
if sameDate(numPeople, numSame): # 10, 20, 40, 100명의 사람 중 생일이 같은 경우
numHits += 1 # 생일은 366일 중 하나일 수밖에 없다
return numHits/numTrials # 사람이 많다면 생일이 겹칠 경우가 증가한다.
import math
for numPeople in [10, 20, 40, 100]:
print('For', numPeople, 'est. prob. of a shared birthday is', birthdayProb(numPeople, 2, 10000))
numerator = math.factorial(366) # 366!
denom = (366**numPeople)*math.factorial(366-numPeople)
print('Actual prob. for N = 100 =', 1 - numerator/denom)수식
$ 1 - {366! \over 366^N * (366 - N)!} $
N명 중 생일이 겹치는 확률 = (1 - N명이 모두 생일이 겹치지 않는 확률) 로 계산한다.
e.g.
$ 1 -{ 366 \times 365 \times 364 \over 366 ^ N } $= 1 - (3명이 서로 다른 생일을 가질 확률)
해당 모델도 마찬가지로 충분한 시행 횟수가 이루어지지 않으면, 추정 확률에 근사도가 떨어진다.
※ 세명이 생일이 같은 확률을 찾고자 한다면 굉장히 복잡한 문제가 된다.
- 모든 생일이 다른 경우
- 한쌍이 일치하고, 나머지가 다른 경우
- 두쌍이 일치하고, 나머지가 다른 경우
- 그외 경우
최적화 모델
- 규범적(Prescripted)
- 예시1) 그래프 노드 A에서 B로 가는 최단 거리 가는 방법(DFS, BFS)
- 예시2) 배낭에서 어떻게 최대의 가치를 얻는다(Knapsack Problem), 결정트리로 도식화 가능
- 그래프와 트리로 모델링 가능
시뮬레이션 모델
- 결과가 이렇다는 것만 말해줌
- 어떻게 그러한 현상이 나타나는 지는 말해주지 않음
- 현실의 근사치(Approximation)
결론
- 시뮬레이션에서 추정확률을 실제 확률 값에 가깝게 하고 싶다면, 시행 횟수를 늘리는 것이 좋다.
Chapter 5. Random Walks
랜덤 워크는 주변 사례를 이해하기 위해 시뮬레이션을 어떻게 사용할 지에 대한 좋은 사례를 제공한다.
e.g.
주식 시장에서 가격의 움직임을 이해
브라운 운동의 이해
술취한 사람이 걸은 걸음의 수와 (출발지점 ~ 도착 지점) 위치가 어떤 관계가 있을까??
※ 위생검사(Sanity Check)
- 무작위 시뮬레이션 모델이지만, 답을 반드시 알 수 있는 경우는 존재하며 해당 테스트 케이스를 이용해 검사하는 것을 뜻한다.
- 예를 들어, 술취한 사람의 걸음 수와 위치의 경우 (t=0 일때 dis = 0)이어야 하며 (t=0, dis = 1) 이어야 한다.
따라서, 반드시 답을 아는 테스트 케이스는 존재하며 해당 검사를 해보는 것을 뜻한다.
시간이 클때는 무작위성이 증가하므로 Sanity Check를 위한 테스트 케이스를 만들어 낼 수 없다.
데이터 시각화를 위한 라이브러리
- Numpy : 선형대수 연산을 위한 라이브러리
- Scipy : 수학 연산을 위한 함수와 클래스를 제공하는 라이브러리
- MatplotLob : 그래프를 그리기 위한 라이브러리
- PyLab : 매트랩에서 제공하는 기능을 제공
class Location(object): # 불변
def __init__(self, x, y):
"""x and y are numbers"""
self.x = x
self.y = y
def move(self, deltaX, deltaY):
"""deltaX and deltaY are numbers"""
return Location(self.x + deltaX, self.y + deltaY)
def getX(self):
return self.x
def getY(self):
return self.y
def distFrom(self, other):
xDist = self.x - other.getX()
yDist = self.y - other.getY()
return (xDist**2 + yDist**2)**0.5
def __str__(self):
return '<' + str(self.x) + ', ' + str(self.y) + '>'
class Drunk(object): #Inherited, 불변
def __init__(self, name = None):
"""Assumes name is a str"""
self.name = name
def __str__(self):
if self != None:
return self.name
return 'Anonymous'
class Field(object): # 딕셔너리, Drunk와 그 위치를 매핑 , 가변
def __init__(self):
self.drunks = {} # key와 value 모두 객체인 딕셔너리 생성
def addDrunk(self, drunk, loc): # drunk와 loc는 둘다 객체
if drunk in self.drunks:
raise ValueError('Duplicate drunk')
else:
self.drunks[drunk] = loc # drunk와 loc는 한쌍이다
def moveDrunk(self, drunk): # 객체를 인자로 받는다
if drunk not in self.drunks:
raise ValueError('Drunk not in field') # 술취한 사람이 영역에 없다.
xDist, yDist = drunk.takeStep()
# use move method of Location to get new location
self.drunks[drunk] = self.drunks[drunk].move(xDist, yDist) # drunk에 매칭 되는 loc 객체를 갱신한다.
def getLoc(self, drunk):
if drunk not in self.drunks:
raise ValueError('Drunk not in field')
return self.drunks[drunk]
class UsualDrunk(Drunk): #상속 받음
def takeStep(self):
stepChoices = [(0,1), (0,-1), (1, 0), (-1, 0)]
return random.choice(stepChoices)
class MasochistDrunk(Drunk): #Bias random walk
def takeStep(self):
stepChoices = [(0.0,1.1), (0.0,-0.9), (1.0, 0.0), (-1.0, 0.0)]
return random.choice(stepChoices)
def walk(field, drunk, numSteps):
"""Assumes: f a Field, d a Drunk in f, and numSteps an int >= 0.
Moves d numSteps times, and returns the distance between
the final location and the location at the start of the
walk."""
start = field.getLoc(drunk)
for _ in range(numSteps):
field.moveDrunk(drunk) # 키(d) 값에 해당하는 Value를 계속 갱신한다.
return start.distFrom(field.getLoc(drunk)) # start도 객체이고, field.getLoc(drunk)이 반환하는 값도 객체이다.
def simWalks(numSteps, numTrials, dClass):
"""Assumes numSteps an int >= 0, numTrials an int > 0,
dClass a subclass of Drunk
Simulates numTrials walks of numSteps steps each.
Returns a list of the final distances for each trial"""
Homer = dClass('Homer') # UsualDrunk 객체 생성, self.name = 'Homor'
origin = Location(0, 0) # Location Object, 처음 시작 위치
distances = []
for _ in range(numTrials): # 100번 시도 한것에 대한 위치를 리스트에 담는다.
f = Field() # Object return
f.addDrunk(Homer, origin) # field의 멤머 변수 딕셔너리를 만든다. drunk와 loc를 각각 Key, Value로 가진다.
distances.append(round(walk(f, Homer, numSteps), 1)) # numTrials --> numSteps
return distances
def drunkTest(walkLengths, numTrials, dClass): # 파이썬은 클래스를 인자로 받는 것이 가능하다.
"""Assumes walkLengths a sequence of ints >= 0
numTrials an int > 0, dClass a subclass of Drunk
For each number of steps in walkLengths, runs simWalks with
numTrials walks and prints results"""
for numSteps in walkLengths:
distances = simWalks(numSteps, numTrials, dClass) # (1, 100, UsualDrunk), (10, 100, UsualDrunk), (100, 100, UsualDrunk), ..., .
print(dClass.__name__, 'random walk of', numSteps, 'steps')
print(' Mean =', round(sum(distances)/len(distances), 4))
print(' Max =', max(distances), 'Min =', min(distances))
random.seed(0)
drunkTest((0, 1, 2, 10, 100, 1000, 10000), 100, UsualDrunk) # Add Sanity 체크
def simAll(drunkKinds, walkLengths, numTrials):
for dClass in drunkKinds:
drunkTest(walkLengths, numTrials, dClass)
random.seed(0)
simAll((UsualDrunk, MasochistDrunk), (1000, 10000), 100)
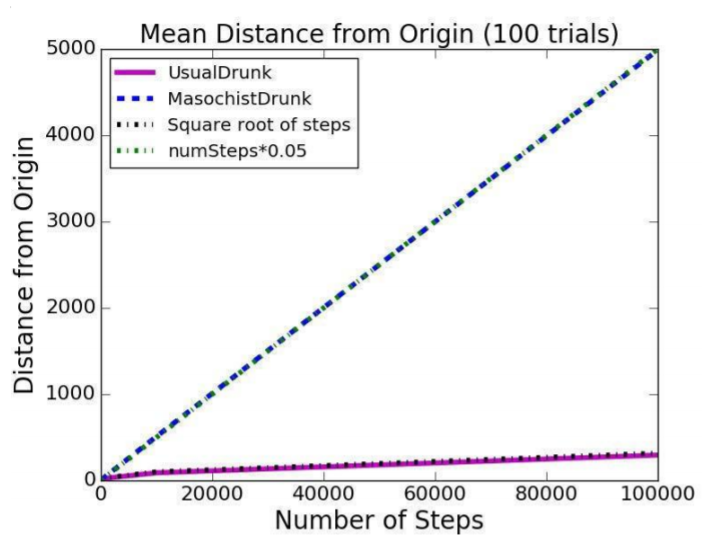

결론
- (아무리 하찮은 것이라도) 현상을 프로그래밍을 이용하여 모델링 할수 있는 가능성을 파악하는 것이 중요하다.
- 시각화를 통해 데이터에 대한 통찰력을 기를 수 있다.
<5강 까지 들으면서 느낀점>
해답을 빨리 얻거나, 많은 풀이 법을 아는 것에서 벗어나
현상을 모델링 해보고, 프로그래밍 하고, 시각화 하면서 예상과 얼마나 유사한지 비교하는 즐거움(?)에 조금 더 초점을 맞춰야 겠다는 생각이 들었다.
[Reference]
[MIT] 데이터 사이언스 기초
https://www.edwith.org/datascience/joinLectures/19265
'데이터 과학 > 데이터 과학' 카테고리의 다른 글
| KL Divergence(Kullback Leibler Divergence) 설명 (0) | 2021.11.01 |
|---|---|
| Density Estimation (in Python) (0) | 2021.03.26 |
| [MIT] 데이터 사이언스 기초 강의 요약[11 ~ 15강] (0) | 2020.11.29 |
| JSON (JavaScript Object Notation) in C (0) | 2020.11.09 |
| [MIT] 데이터 사이언스 기초 강의 요약[6 ~ 10강] (0) | 2020.11.08 |


