Contents
1. 개요
2. 설명
3. TF-IDF
1. 개요
- Bag of Visual Words는 유사 이미지를 찾는 방법 중 하나이다. 이미지 비교에는 픽셀간 비교하는 방법이 있을 수 있고, 소위 이미지에서 'Visual Words'를 구성해 주요 부분만 비교할 수 있다. Bag of Visual Words는 후자의 방법이다.
- Slam에서는 Loop Closing Detection에서 활용된다.
2. 설명
- SIFT와 같은 Descriptor로 이미지의 특징점을 파악한다.
- 특징점을 이용해 이미지를 이른바 시각적 단어의 집합으로 파악하고, 히스토그램을 구성하여 이미지 당 Words의 발생빈도를 통계 낸다.
- 이미지 히스토그램을 이용해 이미지 간의 유사성을 보다 효율적으로 파악한다
(물론 단점도 존재한다. 보완한 것이 아래의 TF-IDF 가중치 변환)
"이미지를 추상화 한다. 계산의 효율을 위해. 위치 정보는 사라진다."
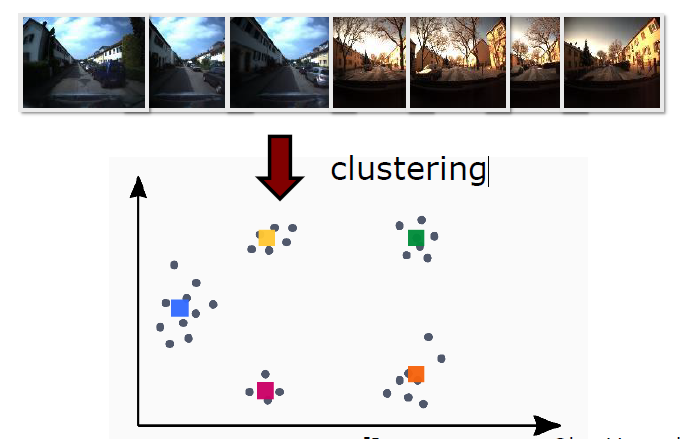
※ 만약 군집화(Clustering)(e.g. K-Means)를 하지 않는다면, 메모리에 쌓아나가는 Words 들이 메모리 용량을 넘게 될 것이다. 그러고 보면 Clustering 성능도 Loop Closing Detection에 영향을 미치게 된다.
3. TF-IDF
3-1. TF-IDF - 계산
- Term Frequency - Inverse Document Frequency
- '히스토그램' 표현 방식의 단점을 보완한 방법
- 너무 자주 나타나는 'uninformative'(정보로 가치가 없는) 것은 downweight 한다. 그리고, Rare한 word는 가중치를 상향한다.
- $$ t_{id} = {n_{id} \over {n_d}} log {N \over n_i} $$
- $ t_{id} $ : Image d에서 i 번째 Word의 히스토그램 Bins
- $ n_{id} $ : Image d 에서 i 번째 Word 빈도
- $ n_{d} $ : Image d 에서 전체 Words의 갯수 (Word 관점)
- $ n_{i} $ : 전체 Image(0 ~ N-1)에서 i Word가 있는 Image 갯수 (Image 관점)
- $ N $ : 전체 Image 갯수
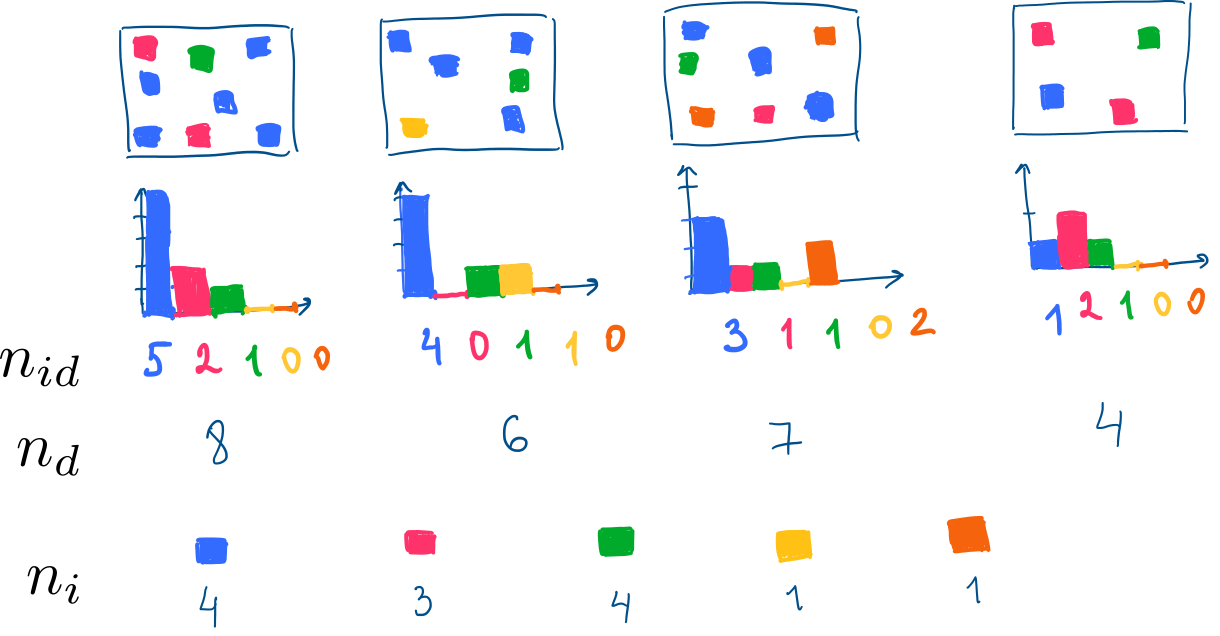
첫번째 이미지를 예로 들면)
파란색 Word는 (해당 이미지에서) 5번이나 등장하므로 가중치가 상대적으로 높다(5/8) : TF, ${n_{id} \over {n_d}}$
하지만, 파란색은 (전체 이미지 관점에서) 자주 등장하는 Word이므로 희귀하지 않는 것이다(log 4/4) : IDF, $ log {N \over n_i} $
| 전체 Image 관점 | $log {N \over n_i} $ |
| 파란색 word | log 4/4 |
| 분홍색 word | log 4/3 |
| 초록색 word | log 4/4 |
| 노란색 word | log 4/1 |
| 주황색 word | log 4/1 |

TF는 히스토그램을 단위 길이로 정규화 하는 역할을 하고,
IDF는 각 Image를 전체 이미지 발생 빈도를 기반으로 가중치 부여하는 역할을 한다.
3-2. TF-IDF - 해석
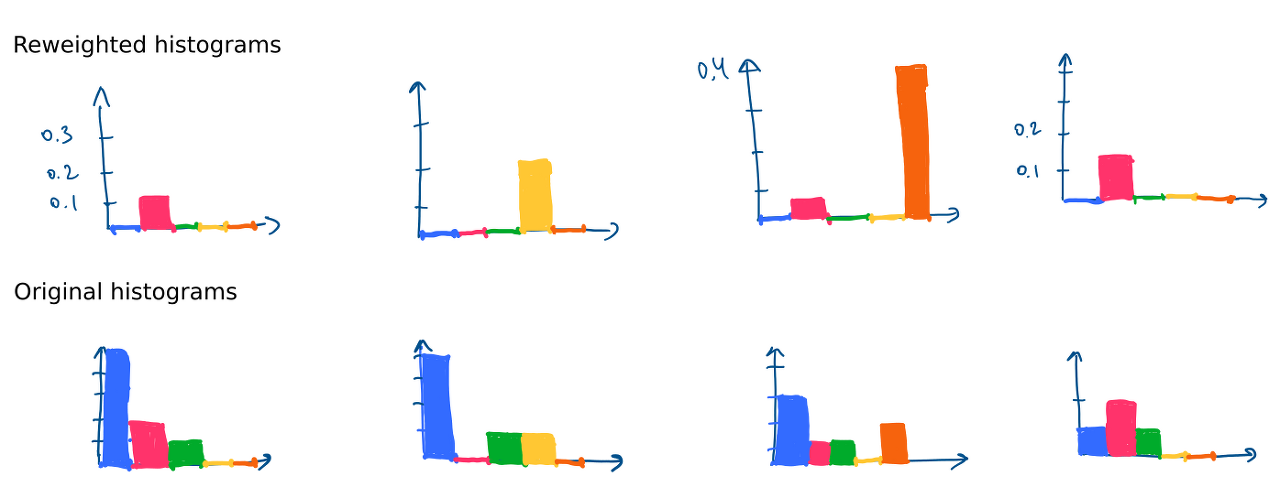
- 파란색은 거의 모든 이미지에서 등장하고, 빈도수도 높지만 '0' 의 값을 가진다.
- 초록색은 빈도수가 낮지만, 거의 모든 이미지에서 등장하기에 '0' 의 값을 가진다.
- 자주 등장하지 않을 때 점수를 높게 받는 듯 하다.
아래는 이미지(0 ~ N-1) 가 유사도를 측정한 것이다(L2, Cosine Similarity 기준으로 각각 비교)
- 값이 작을 수록 유사하다는 뜻이다.
- Cosine Similarity를 기준으로 잡는 것이 조금 더 명확하다(정확히는 Cosine Distance = 1 - Cosine Similarity)
- $$ cossim(x, y) = cos(\theta) = { {x^Ty} \over {||x|| \, ||y||} } $$


3-3. TF-IDF 코드
## weighing tf-idf function
def reweight_tf_idf(histograms):
re_hists = np.zeros(histograms.shape)
N = histograms.shape[0]
n_i = np.sum(histograms > 0, axis=0)
for hist_id in range(histograms.shape[0]):
n_d = np.sum(histograms[hist_id])
for bin_id in range(len(histograms[hist_id])):
re_hists[hist_id, bin_id] = histograms[hist_id, bin_id]/ n_d * np.log(N/n_i[bin_id])
# print(re_hists[hist_id, bin_id], histograms[hist_id, bin_id], n_d, N, n_i[bin_id])
return re_hists
re_hists = reweight_tf_idf(histograms)
Reference
[1] https://github.com/ovysotska/in_simple_english/blob/master/bag_of_visual_words.ipynb
'심화 > 영상 - Algorithm' 카테고리의 다른 글
| Eight Points algorithm(Normalized) - 과제 해결 (0) | 2022.11.19 |
|---|---|
| Hungarian Maximum Matching Algorithm (0) | 2021.01.03 |
| Hausdorff Distance (0) | 2020.12.28 |

